The principal goal of this article is to study the polyhedron called the Rhombic Dodecahedron and to share classroom-tested materials and activities that will engage young students in the study of Mathematics (in particular, polyhedra) in an historical context.
The Rhombic Dodecahedron is a simple, beautiful and interesting polyhedron that can delight young and adults alike.
Johannes Kepler discovered it and we are going to follow Kepler's wonderful mind in our travel exploring its properties in an historical context.
Although we do not know how the Rhombic Dodecahedron was conceived, the first point of view that we are going to develop is fascinating because Kepler described it in relation with the observation of Nature, taking a deep look into how bees build their bee cells.
Kepler's astonishing imagination related this polyhedron with a technical problem: how to pack cannonballs and squeeze them. His proposal of how it is the optimal way to pack spheres is now called 'Kepler Conjecture'.
A third approach could be related with Art because Renaissance mathematicians and artists like Leonardo da Vinci were very near to discover the Rhombic Dodecahedron as a cube with pyramids. But Kepler deserved the merit.
This point of view of the Rhombic Dodecahedron as a cube with pyramids allow us to learn about measures of diagonals, edges, angles and volumes of this polyhedron and other interesting properties.
After this remarkable achievements, Kepler's mind rested? No, not at all. He discovered a second rhombic polyhedron that interested him and he was aware that the cube was a third rhombic polyhedron.
To follow all these ideas is not easy without real mathematical models. A second objective of this article is to encourage readers to build their own polyhedra and to play with them. Building polyhedra is a relaxing activity and the results are appealing because of their beauty. But there is more: we learn mathematical properties of this bodies when we build, look and touch them.
In this article students and teachers will find information and tested resources that can be used in the classroom.
We are going to study a polyhedron called the Rhombic Dodecahedron. This polyhedron is related with some deep questions in Mathemathics (for example, the Kepler Conjecture that we are going to briefly present later) and other fields of science like Crystallography and Chemistry. But, on the other hand, it is a simple and beautiful polyhedron that has a wonderful history that will engage everybody interested in Maths and in polyhedra.
The main goal of this article is to present different approaches to this polyhedron and to share some materials and activities that have been tested in the classroom and in workshops with students in the 11-16 year age group. Text and activities are adapted to this target audience. They Teachers could also be interested in adapting these materials to their own necessities in the classroom.
The Rhombic Dodecahedron is a polyhedron that has twelve equal faces that are rhombi.
The Rhombic Dodecahedron.
It was discovered by the German astronomer and mathematician Johannes Kepler around 1600. Then the first thing that we are going to do is to review some basic facts about Kepler's life and time to put his discovery in an historical context. It is always enriching to be aware that Mathematics is not a finished science. On the contrary, it is a subject in development. With this example of the discovery of the Rhombic Dodecahedron by Kepler we are in a wonderful position to do that.
It is remarkable that there is no notice that nobody before Kepler wrote about this polyhedron. We can be sure that the shape of the Rhombic Dodecahedron was well known: a mineral called garnet has been used since prehistoric times as a gemstone. It is beautiful, abundant and cheap.
But, before Kepler, it seems that mathematicians were not interested in this shape. The most plausible reason may be that this polyhedron is not regular in the sense that interested Greek mathematicians: Its faces are rhombi, not regular polygons, and it does not have just one kind of vertex, unlike Platonic and Archimedean solids.
Garnet with the shape of a Rhombic Dodecahedron.
Following Kepler, we are going to study this polyhedron from different points of view. We are going to relate this polyhedron with Nature, a technical problem and Art. Each approach will teach us some complementary properties of this polyhedron.
The next three sections are the kernel of this article. I have used this material several times and it is always a success. It engage students in the study of Mathematics, because of the beauty of polyhedra and because of the interdisciplinary approach. After a short presentation of the Rhombic Dodecahedron we can talk about its discoverer, Johannes Kepler. Then the description of how bees build their cells is always fascinating. Some interesting properties of this polyhedron could be exposed. After that, we can build a cardboard Rhombic Dodecahedron or a model of a bee cell. Each student has his own beautiful polyhedron that, for sure, will remind him or her some properties of this body. Another possibility to finish the session is to glue all the Rhombic Dodecahedra to show how this polyhedron tessellate space. One a a half or two hour workshop is a wonderful experience for all students. Building polyhedra using simple techniques is the key of the activity. It is rewarding not only for its aesthetic appeal. Perhaps touching and manipulating these models is the best way to learn and understand the properties of these bodies.
When Kepler studied the optimal packing of spheres he found that the Rhombic Dodecahedron can be generated compressing thirteen cannonballs. It is very easy to reproduce this experiment using clay balls and the result astonishes the audience.
These are some of the activities that are proposed in this article. There are more, with different levels of difficulty, that can be adapted to our students.

Panoramica of the exhibition 'Kepler, honeybees and the Rhombic Dodecahedron' (2020, Alcalá de Henares, Spain).
Johannes Kepler (1571-1630) was a German scientist, mathematician, astronomer, and astrologer. He lived in a time full of new ideas and discoveries.
During the sixteenth century and early seventeenth century, the Greek mathematical masterworks, such as Euclid's Elements, the Conics of Apollonius or the works of Archimedes, were studied seriously. Geometry interested not only scientists but also artists and craftsmen.
Perhaps one of the most important new ideas that influenced Kepler's work was Copernicus' sun-centered cosmology. The publication of Copernicus' book 'De Revolutionibus' in 1543 started what we call the Copernican Revolution. His observations supported the idea that the Earth and all planets revolved around the Sun. His heliocentric theory implied that the Earth was not the stationary center of the universe. Since his youth, Kepler was an early supporter of Copernicus' heliocentric model.
The following image is a very basic timeline about Kepler and his time. The aim is to provide some historical context. The main idea that it try to convey is that Kepler lived in a time between the Renaissance and the great discoveries of Newton and Leibniz.
The Renaissance is a period in European History that can be seen as a transition between the Middle Ages and modernity. More people could access old and new ideas thanks to the printing press (Gutenberg, c.1400-1468). Artists developed new techniques (for example, the use of perspective). Times of religious changes such as the Protestant Reformation (Luther, 1483-1546) and the european exploration of the world.
The most famous scientific of Kepler's contemporaries was Galileo (1564-1642).
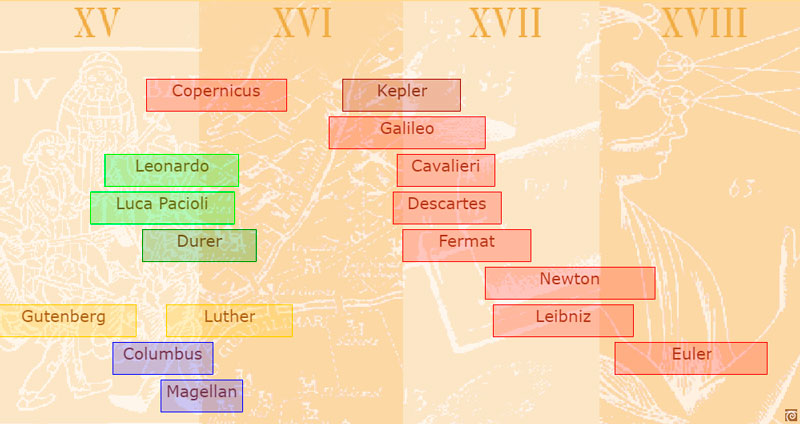
Basic timeline about Kepler and his time. Kepler was a man between the Renaissance and the great discoveries of Newton and Leibniz.
Johannes Kepler was born in Weil der Stadt in 1571. His parents were poor. He was an intelligent boy with a delicate health. Throughout his life he had to change his place of residence several times: he studied at the University of Tübingen, was appointed as a mathematics teacher in Graz, then he worked with the famous astronomer Tycho Brahe (1546-1601) in Prague where Kepler became Imperial Mathematician, after that he had to move to Linz and Sagan. He died in Regensburg in 1630.
His life was not easy and he live in very troubled times. He struggled with his bad health, his financial troubles and family difficulties. He was affected by religious conflicts (Kepler was a very religious man) and even war (the Thirty Years war, that devastated Germany, broke out in 1618).
Despite all these circumstances, Kepler was able to make important contributions to science, in particular to Astronomy, Mathematics and Optics.
As an astronomer, Kepler is famous because of his discovery of the three laws of planetary motion now known as Kepler's Laws. Newton later showed that Kepler's laws could be deduced from Newton's laws of motion and universal gravitation law.
As a mathematician, Kepler discovered two new regular polyhedra (today called the great and small stellated dodecahedron), two new rhombic polyhedra (the Rhombic Dodecahedron and the Triacontahedron), worked on the problem of close packing of equal spheres, was interested in logarithms and found volumes of solids of revolution.
Because of his contributions to the development of calculus and his interest in polyhedra, Kepler extended Archimedes' results and can be seen as a precursor of the important discoveries made by Newton and Leibniz.
Kepler enjoyed a fertile imagination. As an example, we can consider how a simple anecdote led him to think about the volume of solids: During his second wedding, Kepler was surprised at how the merchant measured the volume of wine barrels. As a result, Kepler studied how to calculate the volume of solids of revolution.

|
Kepler: The Volume of a Wine Barrel
To learn more about Kepler contribution to the development of calculus we can read this article published in 'Convergence: Where Mathematics, History, and Teaching Interact'. |
Another anecdote was the origin of the book that is our main source about his discovery of the Rhombic Dodecahedron.
The title of the book is 'Strena Seu De Nive Sexangula' ('The Six-Cornered Snowflake. A New Year Gift', Prague, 1611). It was written as a New Year gift to his friend and benefactor Matthew Wacker von Wackenfels.
Kepler wrote that he was thinking and walking along the Charles Bridge one winter day in Prague and
just then, by a happy occurrence, some of the vapor in the air was gathered into snow by the force of the cold, and a few scattered flakes fell on my coat, all six-cornered, with tufted radii. By Hercules! Here was something smaller than a drop, yet endowed with a shape. Here indeed, was a most desirable New Year's gift for the lover of Nothing, and one worthy as well of a mathematician (who has Nothing, and receives Nothing) since it descend from the sky and bears a likeness to the stars. [Kepler. The Six-Cornered Snowflake, English translation by Jacques Bromberg, p. 33]
He tried to explain the reason for the six-angled shape of snow crystals but his rich fantasy flew from honeycombs to pees, from pomegranates to cannonballs and, in the middle of his thoughts, a new polyhedron was described by him: the Rhombic Dodecahedron.
This beautiful book was written in Prague and published in Frankfurt am Main in 1611. First editions of this book are very rare. We can enjoy some images of a first edition in the article Convergence. Mathematical Treasure: Kepler and Sphere-packing by Frank J. Swetz.
In this article we are going to follow Kepler's thoughts about this polyhedron, how he recognized it looking into the bottom of bee cells and how we can understand its main properties intuitively.
Since its origins, Humanity has observed Nature and has been fascinated by the perfection and beauty of honeycombs.
Bee cells with its hexagonal structure
Pappus of Alexandria (around the year 320) was interested in this subject from a mathematical point of view. In the preface of his 'Mathematical Collections', Book V. he considered how bees build their honeycombs and he wrote:
...first collecting the sweets of the most beautiful flowers which grow on the earth, they make from them, for the reception of the honey, the vessels which we call honeycombs, (with cells) all equals, similar and contiguous to one another, and hexagonal in form. And that they have contrived this by virtue of a certain geometrical forethought we may infer in this way. They could necessarily think that the figures must be such as to be contiguous to one another, that is to say, to have their sides common, in order that no foreign matter could enter the interstices between them and so defile the purity of their produce. Now only three rectilinear figures would satisfy the condition, I mean regular figures which are equilateral and equiangular; for the bees would have none of the figures which are not uniform... There being then three figures capable by themselves of exactly filling up the space about the same point, the bees by reason of their instinctive wisdom chose for the construction of the honeycomb the figure which has the most angles, because they conceived that it would contain more honey than either of the two others. [Heath. A History of Greek Mathematics.Vol II, p. 390].[You can read more about Pappus in note 16 of Kepler's book 'The Six Cornered Snowflake', p. 141. Notes by J. Bromberg and G. Bleichmar].
In this famous paragraph, Pappus deals with two main ideas. One is the comparison of the areas or volumes of figures of the same perimeter or surface area. This is a kind of problems of optimization that we call isoperimetric problems. Are bees so clever that they spend the less amount of wax to build their honeycombs?. This kind of questions are usually difficult.
The second one is more basic. He wrote about 'plane tessellations', it is to say, how we can fill the plane with equal and regular polygons.
The following image is an artistic approach to these kind of tessellations. One based in the equilateral triangle (Alhambra of Granada), the second has a square grid (The Royal Alcazar of Seville) and the third, based in hexagons, was designed by the architect Antoni Gaudi (Barcelona).

Three artistic examples of plane tessellations.
The same idea but applied to the space, it is to say 'space tessellations' will play an important role in our study of the Rhombic Dodecahedron. The question is: how we can fill space using equal polyhedra?. Although the question is not simple, we have a first and simple answer: the cube tessellate space.
That bees use a hexagonal tessellation to build their honeycombs was a well known fact. But more than one thousand years after Pappus, Kepler had the wisdom to look at the bottom of the cell!
Honeycomb and the bottom of cells.
We can follow how new ideas were born in Kepler's great inventive mind reading his book 'De nive sexangula' ( 'The Six-Cornered Snowflake'). About the structure of the honeycomb, Kepler wrote:
If you should ask the geometers on what plan the cells of bees are built, they will replay, on a hexagonal plan. The answer is clear from a simple look at the openings or entrances, and the sides that form the cells. Each cell is surrounded by six others, and is divided from the next by a shared side. But if you observe the bottom of each cell, you will notice that it slopes into an obtuse angle formed by three planes. This bottom (which you might call the "keel") is joined to the six sides of the cell by six other angles, three higher ones that are trilateral, just like the bottom angle of the keel, and three lower ones, in between, that are quadrilateral. [...] The three planes of the keel are identical to one another, and their shape is what geometers call a rhombus. [Kepler. The Six-Cornered Snowflake, p. 37 and 43]
The following drawing is from Kepler's 'Harmonices Mundi' ('The Harmony of the World', Linz, 1619)), another of his most important books. There he draw a polyhedron made of a belt of six rhombi (we can imagine these six rhombi on the walls of the hexagonal prism of the cell), then he added three rhombi in the same way that bees close their cells (the 'keel') and he closed the polyhedron with three more rhombi (bees does not close the cell, they need an open entrance).
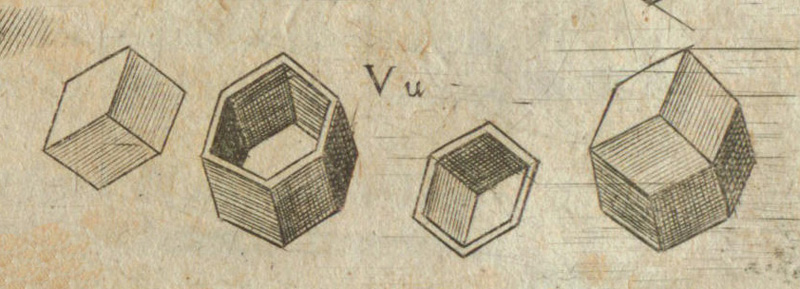
Rhombic Dodecahedron drawing from Kepler's book 'Harmonices Mundi'
What properties can we deduce from this description of the Rhombic Dodecahedron?
The Rhombic Dodecahedron has 12 rhombic faces and 24 edges.
It has six vertices at which four edges meet (the angles of the rhombi are acute) and eight vertices at which three edges meet (the angles of the rhombi are obtuse).
Six rhombi form a belt. These six rhombi are the rhombi put in the faces of the hexagonal prism. In fact, the Rhombic Dodecahedron has four belts of six rhombi.
The angle between two adjacent faces of these six rhombi that form a belt is 120º. It can be proved that the angle between two adjacent faces of the Rhombic Dodecahedron is 120º.
If we imagine a layer of bee cells we can put inside each cell a Rhombic Dodecahedron. Then we can imagine an infinite layer of Rhombic Dodecahedra.
Kepler went beyond and wrote:
It should also be observed that the cells are arranged in two layers, with the openings facing oposite directions; the backs adjoining one another and closely packed; and the corner of each keel in one layer fitted into the three corners of the three keels in the other. By this workmanship, not only does each cell share six sides with the ones surrounding it in the same layer, but also three planes at the bottom with three other cells from the opposite layer. Thus, each bee has nine neighbors, with each of whom it shares a dividing wall. [Kepler. The Six-Cornered Snowflake, p. 43]
Then you can imagine that inside this second layer of hexagonal cells you can put another layer of Rhombic Dodecahedra.

Bee cells in two layers.
Why not to put a third and a four layer, an so on? You can see that the Rhombic Dodecahedron has a surprising property: Rhombic Dodecahedron tessellate space. Kepler was aware that the way that bees build their cells lead as to a polyhedron that tessellate space.
TO INVESTIGATE
Isoperimetric problem.
Using derivatives we can solve an isoperimetric problem that interested 18th century mathematicians like Colin Maclaurin.

|
Honeycomb: a property of minima
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?. |
We will see that Kepler had a deep understanding of the properties of the Rhombic Dodecahedron and how his creative mind thought about it from different points of view. But before we will return to explore Kepler's approaches it could be an inspiring idea to build some models of this wonderful polyhedron.
To enjoy this polyhedron, to learn more about it and to convince ourselves of its beautiful properties it is highly recommendable to build a Rhombic Dodecahedron.
Here we recommend to build a Rhombic Dodecahedron made of cardboard. It is a beautiful little box designed by John Jeremiah Edminster and one variant that is a box with the shape of a bee cell.

Two models to build with cardboard: a bee cell and a Rhombic Dodecahedron. Design: John Jeremiah Edminster.
This two models are little boxes. Design: John Jeremiah Edminster.
You can download, print, cut and glue this net of a Rhombic Dodecahedron. Looking at this net you can see the horizontal distribution of six rhombi that you must glue making a belt, three rhombi above and three rhombi below close the polyhedron.
Net of a Rhombic Dodecahedron. Used with permission of the designer, John Jeremiah Edminster.
The following is a net of a box that it is a model of a bee cell.
Net of a bee cell. Used with permission of the designer, John Jeremiah Edminster.
If we build several of these polyhedra we can explore how bees make their honeycombs and the property of the Rhombic Dodecahedron to tessellate space. We are going to learn more about that later.
From my own experience, I could say that a workshop with the material exposed so far in this article it is always a success with young students. Honeybees are fascinating and the model is easy to build, simple, beautiful and interesting.
Years after I started building these models with students it was a pleasure to read an old article, written in 1936 by W. Hope-Jones, in the best tradition in teaching. The title of this inspirational article is 'The Rhombic Dodecahedron for the Young' and it is full of good ideas and written with enthusiasm:
This interesting solid has tended too much in the past to be classified as 'for adults only' (and for not too many of them); but because it supplies the answer to a question which every intelligent youngster asks himself, I think it is worth while to try and smooth the path of any teacher who wants to let childer to (say) 13 share in some of its treasures.
The bee's cell is very well worth doing for its own sake, in addition to its value as leading up to the Rhombic Dodecahedron. Designing it on the flat is our job; but cutting out a given design and gumming it up into its three-dimensional shape is excellent fun for children. [Hope-Jones. The Rhombic Dodecahedron for the Young].
Reading Kepler's book 'De Nive Sexangula' is an enriching experience. Not only because of the ideas that he is writing about but also because the author is describing how his creative mind is working. It is an opportunity to have a sense of the mind of a genius in action!
After his detailed description of how bees close their cells and its connexion with the Rhombic Dodecahedron, his mind seemed to jump from topic to topic without apparent connection. He took a look at pees and the seeds of pomegranates. He noticed that these seeds, when they grow, are squeezed into shapes that have rhombic faces.

Pomegranate seeds with rhombic faces.
From these examples inspired in Nature, his train of thought made what it seems a radical change. Now he wanted to discuss a technical problem: how is the best way to pile up cannonballs?
How Kepler is going to link honeycombs and the seeds of pomegranates with this technical problem? We are going to see right now.
Kepler may have became interested in the question of the stacking of spheres because of Thomas Harriot (c.1560-1621).
Thomas Harriot was an English mathematician, astronomer and a friend and adviser to Sir Walter Raleigh (c.1552-1618). The later asked Harriot to solve several problems about the stacking of cannonballs because, as an a sea explorer, he was interested in this practical problem. Harriot could solve them and, more than that, he considered the connection with the atomic theory. Harriot is considered nowadays one of the greatest mathematicians of his time. The range of his interests was wide: Mathematics (he made important contributions to algebra), Optics, Astronomy (he build telescopes and made observations).
We are not sure if Harriot shared with Kepler the problem of the best way to pack cannonballs. We know that they exchanged a few letters being Optics the main subject of their correspondence. It was very common in those days to exchange letters between friends and colleagues and Kepler corresponded with many people.
Anyway, Kepler was interested in the problem of stacking spheres and wrote about this issue in 'De Nive Sexangula'. We are going to see how Kepler related this questions with the Rhombic Dodecahedron
A stack of cannonballs.
Kepler wrote:
In general, spheres of equal size will arrange themselves in one of two ways when placed in a container, corresponding to the two ways in which they can be arranged on a plane.
For if you take a number of spheres of equal size scattered over a horizontal plane and gather them into a small space so that they touch one another, they will come together either in a triangular or in a square arrangement. In the first case, each is surrounded by six others; in the latter, by four; and the pattern of contact is everywhere the same, except for the spheres on the edges. A pentagonal arrangements fails to produce a uniform distribution, while a hexagonal arrangement can be resolved into triangles. Thus, only the two aforementioned arrangements are possible.[Kepler. The Six-Cornered Snowflake, p. 55]
We can start with a triangular or a square arrangement and put more layers of spheres in the holes, like a grocer organize oranges. Then Kepler notice three things:
1) These two arrangements that seems different are equal. In both cases each sphere is surrounded by other twelve.
There can be no triangular ordering without the square and vice versa. [Kepler. The Six-Cornered Snowflake, p. 59]
This is not inmediately obvious but the following video is a good visual explanation:
There can be no triangular ordering without the square and vice versa. Filmed in the workshop of the ceramist Luis Larriba in Tartanedo (Guadalajara, Spain).
2) These are the tightest possible solid arrangements of spheres, that wastes the least amount of space. This claim became known as Kepler Conjecture. It was proved by Thomas Hales in 1998 with the help of computers.
3) When compressed the spheres become rhombic. Only a very creative mind could have think about squeezing iron balls!
Was Kepler right? To squeeze iron balls is difficult but we can make this easy and surprising experiment using clay. We need thirteen balls, we will put them in the following disposition and then we will squeeze them carefully ...

Preparation for the experiment of compressing spheres.
...and we get a Rhombic Dodecahedron. Easy and surprising!
This was the incredible connection that Kepler found between how bees close their cells, how the seeds of pomegranates grow and how is the best way to pile up cannonballs. He was inspired by Nature and by a technical problem and he was able to mix these two worlds wonderfully.
The central sphere after squeezing: a Rhombic Dodecahedron.
If we imagine that we squeeze hundreds of balls in this way we can think that we will get a lot of Rhombic Dodecahedra. We could conclude again that the Rhombic Dodecahedron tessellate space.
Perhaps it is the right moment to go back to honeycombs and to look for a physical and plausible explanation of how bees build their cells.
In his very well documented book 'On Growth And Form', D'Arcy Thompson wrote:
The most famous of all hexagonal conformations, and one of the most beautiful, is the bee's cell. As in the basalt or the coral, we have to deal with an assemblage of co-equal cylinders, of circular section, compressed into regular hexagonal prisms; but in this case we have two layers of such cylinders or prisms, one facing one way and one the other, and a new problem arises in connection with their inner ends. We may suppose the original cylinders to have spherical ends, which is their normal and symmetrical way of terminating; then, for closest packing, it is obvious that the end of any one cylinder in the one layer will touch, and fit in between, the ends of three cylinders in the other. It is just as when we pile round-shot in a heap; we begin with three, a fourth fits into its nest between the three others, and the four form a "tetrad", or regular tetragonal arrangement.
Just as it was obvious, then, that by mutual pressure from the sides of six adjacent cells any one cell would be squeezed into a hexagonal prism, so is it also obvious that, by mutual pressure against the ends of three opposite neighbours, the end of each and every cell will be compressed into a trihedral pyramid. [D'Arcy Thompson. On Growth And Form, p. 525]
After doing this experiment with balls we are in a wonderful position to talk about another beautiful polyhedron: the Cuboctahedron.
Kepler was very interested in polyhedra. In his book 'Harmonices mundi' ('The Harmony of the World', 1619) he studied the thirteen Archimedean solids and he made several discoveries in this field.
One of the Archimedean solids is called the Cuboctahedron. This beautiful polyhedron was known since prehistoric times and used in jewelry and decoration. It has a close relation with the Rhombic Dodecahedron and our experiment with balls.
If you put twelve balls surrounding a center ball as before we could see that these twelve balls are in a regular disposition. They are in the vertices of a Cuboctahedron.
Spheres and Cuboctahedron. The Cuboctahedron is an Archimedean solid.
The Cuboctahedron has 8 equilateral triangles and 6 squares as faces. Notice that the Rhombic Dodecahedron have 14 vertices. This is not a coincidence.
Its twelve vertices correspond with the twelve faces of the Rhombic Dodecahedron.
Among other interesting properties, the Cuboctahedron has 24 edges that are distributed in four regular hexagonal sections. Do you remember the belts of six rhombi that our Rhombic Dodecahedron has? It has four belts and each one of them correspond with one of the four hexagonal sections of the cuboctahedron.
A Cuboctahedron inside a Rhombic Dodecahedron. Cardboard and plastic. Vertices were 3d printed.
TO INVESTIGATE
To learn more about this fascinating polyhedron it is highly recommended to build one model.
We can get a cuboctahedron by cutting the vertices of a cube or an octhaedron. This process is called 'truncation'.

|
Properties of the cuboctahedron.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube. We study some of its properties. This beautiful polyhedron is used as a decoration, in Art and jewelry. |
More images and instructions about the experiment of the clay balls and some properties of the cuboctahedron.

|
More about Kepler and cannonballs.
Centers of the twelve balls surrounding one central ball are vertices of a cuboctahedron. |
If we play with balls we will easily realize that there is a second way to put twelve balls surrounding another.
Squeezing this second organization we will get a different polyhedron that is called Trapezo-Rhombic Dodecahedron.
Trapezo-Rhombic Dodecahedron. Cardboard and magnets.
TO INVESTIGATE
The Trapezo-Rhombic Dodecahedron is a polyhedron that also tessellate space.
|
|
Trapezo-Rhombic Dodecahedron.
The Trapezo-Rhombic Dodecahedron has twelve faces but six of them are trapezoids. |
Before we present a third point of view about the Rhombic Dodecahedron that Kepler taught us we have a good opportunity to see how Renaissance artist were interested in polyhedra and that they almost got the Rhombic Dodecahedron.
During the Renaissance, good translations of the classics were widely available. Artists, scientists and craftsmen were interested in Mathematics and, in particular, in polyhedra. They found them to be beautiful objects to be depicted in their artwork and good examples to practice the new technique of perspective.
The study of this explosion of interest in polyhedra after the 15th century is a good opportunity to mix History, Art and Geometry. [See Cromwell's Polyhedra and Pedoe's Geometry and the Liberal Arts].
For example, Albrecht Dürer(1471-1528) was the first to publish plane nets of polyhedra. Nowadays it is very typical to build polyhedra using plane nets and we are very use to it. It was Dürer the first to publish this way to give information in a flat format about a three-dimensional body.
The following drawing is the net of a Cuboctahedron that he published in his book 'Underweysung Underweysung der Messung' (Nurember, 1525).
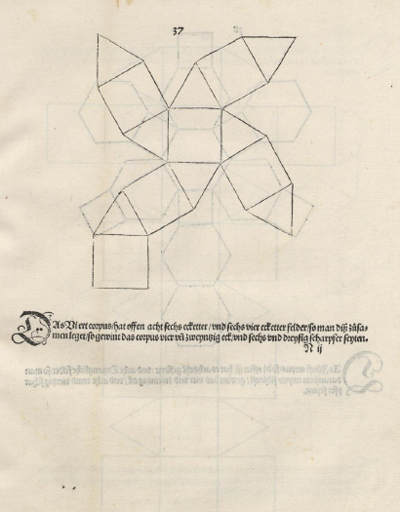
Dürer. Plane net of a Cuboctahedron.
They knew how to generate new polyhedra cutting the vertices of other polyhedra. This process is called 'truncation'.
Leonardo da Vinci draw beautiful images of polyhedra for Luca Pacioli's book 'De Divine Proportione' (Venice, 1509).
The following video is inspired in Leonardo's work depicting a Cuboctahedron:
A second procedure they use to build new polyhedra was to add pyramids to the faces of a polyhedron. Pacioli called this kind of new polyhedra 'elevatus'. We can use words like 'augmented' or 'raised'.
If we add six pyramids to a cube we get a new polyhedron that has 24 triangular faces.
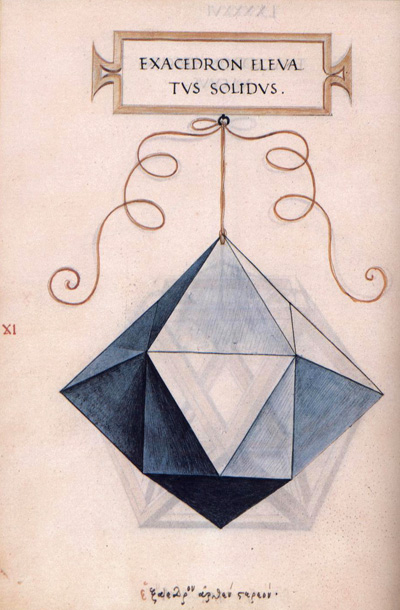
With permission of Editorial Akal. Edition of Pacioli's book 'La Divina Proporción'.
This polyhedron is very near our Rhombic Dodecahedron. They almost got it, our polyhedron is there, in front of their eyes, like the garnets. But the merit of the discovery of a new rhombic polyhedron is for Kepler.
Perhaps the most relevant difference between Renaissance artist and Kepler is that whereas they usually augmented a polyhedron with equilateral pyramids, Kepler was looking for some regularity of the resulting polyhedron instead, rather than that the pyramids where regular. As a mathematician, he was much more systematic in his study of polyhedra and his pursuit for regularity. For example, before Kepler only some of the Archimedean solids were described but it was Kepler who rediscovered the complete set of the thirteen Archimedean solids.
TO INVESTIGATE
More about Leonardo da Vinci drawings of polyhedra.

|
Leonardo da Vinci: Drawing of an stellated octahedron (stella octangula) made to Luca Pacioli's De divina proportione.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula). |

|
Leonardo da Vinci: Drawing of a cuboctahedron made to Luca Pacioli's De divina proportione.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron. |

|
Leonardo da Vinci:Drawing of an augmented rhombicuboctahedron made to Luca Pacioli's De divina proportione.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the augmented rhombicuboctahedron. |
We have already seen two different approaches that Kepler used to study the Rhombic Dodecahedron.
Firstly, he saw this polyhedron looking into how bees build their cells. He was inspired in Nature.
Secondly, he found the Rhombic Dodecahedron as a result of squeezing cannonballs. That was related with a technical problem.
These two points of view are wonderful examples of Kepler's creative mind. But if we want to get a deeper understanding of the Rhombic Dodecahedron, what is the shape of its rhombi, the length of the two diagonals, the measure of the angles and the volume of this polyhedron, another approach would be very helpful.
And was Kepler, one again, who gave us the simplest way to see the Rhombic Dodecahedron, the way to make basic calculations about it and to find another beautiful explanation of the property that this polyhedron tessellate space.
The key was that Kepler understood that the Rhombic Dodecahedron can be seen as an 'elevatus' cube, a cube with six special pyramids attached.
In his book 'Epitome Astronomiae Copernicanae' (printed in Linz between 1618 and 1621) he wrote about the Rhombic Dodecahedron again and draw the following clarifying picture:
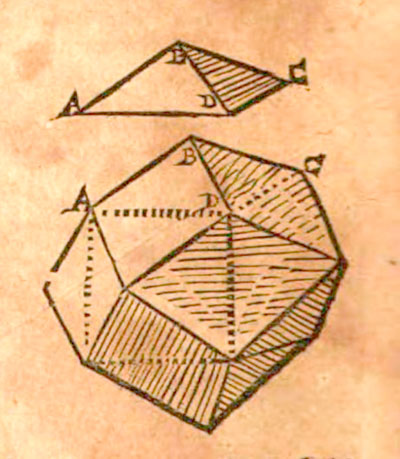
Kepler: Epitome Astronomiae Copernicanae. A cube with pyramids.
In the following video we can see how changing the hight of the pyramids attached to a cube we get different polyhedra with 24 triangular faces. But, to a precise hight, pairs of neighboring triangular faces lie in the same plane and become rhombi.
This is the easiest way to see the Rhombic Dodecahedron. This point of view allow us to learn more properties of this polyhedron.
A cube with pyramids. Cardboard and magnets.
What consequences we can get from this approach?
1) First, we can inscribe a cube inside a Rhombic Dodecahedron.
A cube and an octahedron inside two Rhombic Dodecahedra.
Notice that the cube is produced linking the eight vertices where three edges meet.
Which polyhedron we get when we link the six vertices where four edges meet?.
2) Second, we can calculate some basic measurements about diagonals and the length of the edge.
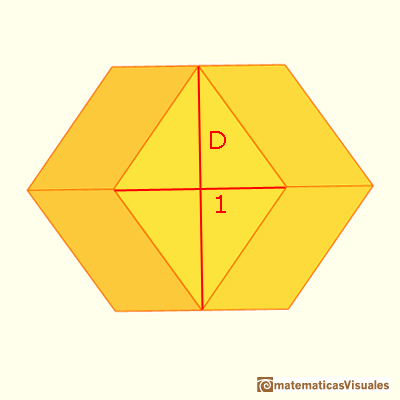
That height of that pyramid is not very difficult to calculate. We can suppose that the length of the cube side is 1. Then:
We can also calculate the length of D:
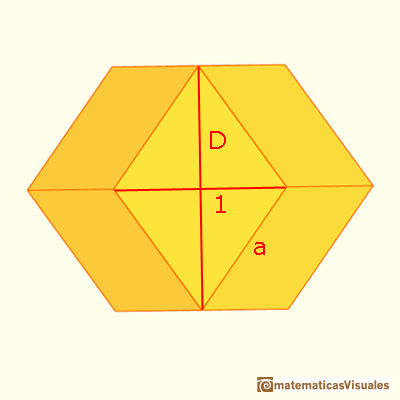
Our rhombuses have two diagonals: the measure of the short one is 1 and the other is D.
We can calculate the length of the side a:
TO INVESTIGATE
We need some basic trigonometry to calculate angles of the faces of the Rhombic Dodecahedron.
The obtuse angle is called Maraldi Angle.

|
Angles of the rhombic faces of a Rhombic Dodecahedron.
Giacomo Maraldi was the first mathematician to study and publish about the angles of the rhombi at the bottom of bee cells. |
3) There is a basic relation between the volume of the Rhombic Dodecahedron and the volume of the inscribed cube.
We notice that these six pyramids are pyramids that you can put inside a cube. Six vertices of these pyramids joint in the center of the cube.
Watching the following video you will see another approach to this relation between the cube and the Rhombic Dodecahedron:
It is not difficult to build a model of this construction using cardboard (with magnets inside):
A cube with pyramids. Cardboard and magnets. A section of the cube.
Now we can study the volume of a Rhombic Dodecahedron.
If we write the volume of the Rhombic Dodecahedron as a function of the edge length:
The volume of the Rhombic Dodecahedron is double the volume of the inscribed cube.
4) We can tessellate space with Rhombic Dodecahedra.
Hugo Steinhaus described this property in a simple and precise way:
We have already mentioned tilling the whole of space with cubes. We can get another filling of this sort by the following procedure: we make the cubes alternately black and white to get a kind of chessboard and then we remove the black ones. We decompose each void space into 6 pyramids on square bases with a common vertex in the certer of the void space. If we consider a single white cube with 6 pyramids based on it, we see a rhombi dodecahedron with a cube inscribed in it. It is obvious that by our procedure we have filled the whole of space with congruent rhombic dodecahedra.(...) The vertices are of two kinds: (1) where 4 solids meet; (2) where 6 solids meet. [Steinhaus. Mathematical Snapshots. p.185].
Kepler was well aware of this property. For example, he wrote en his book 'The Six-Cornered Snowflake':
[The Rhombic Dodecahedron] shares this property with the cube: that just as eight corners of eight cubes brought together at a single point will fill the space entirely and leave no gap, so will the corners of the first kind of rhombic figure, when four of the obtuse (trilateral) angles or six of the quadrilateral angles come together. Thus, a space con be completely filled just with rhombic figures of tis kind, as long as four three-sided angles or six four-sided angles alway come together at a single point, so that a solid whole is made. [...]"
This, then, is the geometric figure closest to a regular solid that fills a space entirely, just as the hexagon, the square, and the triangle fill a plane. It is the very shape that bees produce in their honeycombs, except for the fact that their cells lack a roof to match the bottom. [Kepler. The Six-Cornered Snowflake, p. 45]
TO INVESTIGATE
With all the information we have about the Rhombic Dodecahedron we can calculate the density of the optimal sphere packing perhaps in the easiest possible way.
|
|
Density of the optimal sphere packing.
Using the Rhombic dodecahedron as a unit cell it is not difficult to calculate the density of the optimal sphere packing. |
The best way to understand three-dimensional bodies is to build some models. As a complement to our construction of a Rhombic Dodecahedron we can build more polyhedra.
We already know that we can put a cube inside a Rhombic Dodecahedron. The vertices of this cube are the vertices of the Rhombic Dodecahedron that join three rhombi.
A cube inside a Rhombic Dodecahedron.
You can download, print, cut and glue this net of a cube to put inside our Rhombic Dodecahedron. Yo do not need to change the scale because it will fit perfectly well inside our polyhedron.
Net of a cube to put inside the Rhombic Dodecahedron.
Inside the cube we can put a beautiful piece of origami, an Omega Star. That omega star has the structure of a Cuboctahedron. It is easy and a real pleasure to fold this example of modular origami. Highly recommended!
In the template is depicted the right size of the six pieces of paper you need to build the origami star.
Rhombic Dodecahedron, a cube and an Omega Star (a cuboctahedron).
With a bit of imagination you could see that the twelve vertices of the omega star (cuboctahedron) are located at the centers of the rhombic faces.
The Rhombic Dodecahedron has six vertices were four rhombi met. This vertices are also the vertices of an octahedron that we can put inside our Rhombic Dodecahedron.

An octahedron inside a Rhombic Dodecahedron.
Net of an octahedron to put inside the Rhombic Dodecahedron.
Kepler discovered the Rhombic Dodecahedron observing the base of bee cells. That was a wonderful birth of a new polyhedron. Then he showed us that this Rhombic Dodecahedron was related with a technical problem: how to pile up cannonballs. After that he taught us the simplest way to understand the Rhombic Dodecahedron, as a cube with pyramids. He knew that this polyhedron, as the cube, tessellate space.
Was his mind at rest after these discoveries?. No, not at all.
Kepler wrote:
Intrigued by these rhombi [the rhombi from the bottom of bee cells], I began looking into geometry to see whether a body resembling the five regular solids and the fourteen (13) Archimedean solids could be constructed exclusively from rhombi. I discovered two, one related to the cube and the octahedron, the other to the dodecahedron and the icosahedron. (The cube itself can be considered a third, since it is like two tetrahedra joined together) The first of these solids is contained by twelve rhombi, the other by thirty. [Kepler. The Six-Cornered Snowflake, p. 43 and 45 ]
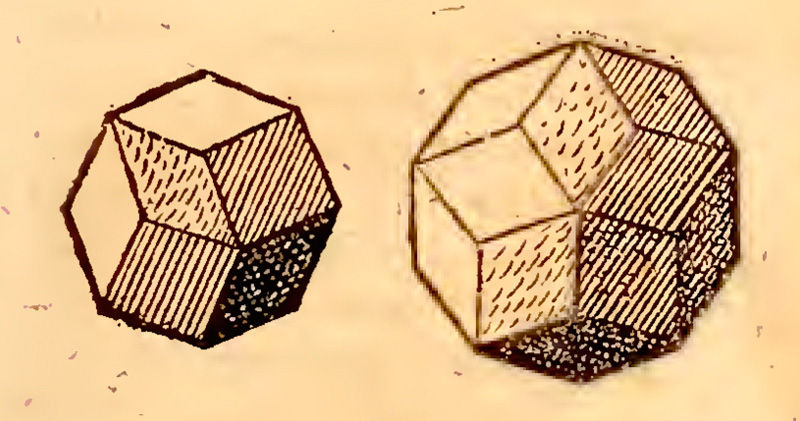
Rhombic dodecahedron and rhombic triacontahcdron, from Harmonices Mundi Book II, p. 61.
The second rhombic polyhedron that Kepler discovered, with thirty faces, is called Triacontahedron.
Three rhombic polyhedra: Rhombic Dodecahedron, Triacontahedron and cube.
Which are the relations between this two rhombic polyhedra?
How could Kepler's mind discover the Triacontahedron after discovering the Rhombic Dodecahedron?
It is only the cube the third rhombic polyhedron because its six faces are square, it is to say, an special kind of rhombus? Or there is a deepest connection between these three rhombic polyhedra?
The study of the Triacontahedron and the answer to these questions deserve another article!
The Rhombic Dodecahedron is a simple and beautiful polyhedron. It is easy to put this body in an historical context because we know its discoverer: Johannes Kepler. To show that Mathematics is a science in progress is one of the goals of this article.
In different occasions Kepler wrote about this polyhedron and showed us complementary approaches. He saw this polyhedron at the bottom of bee cells. He understood its relation with the difficult problem of the best way of packing spheres (Kepler's Conjecture) and was aware that it shares with the cube the property of tessellate space.
Then, the Rhombic Dodecahedron is related with the observation of Nature, some Technical and Mathematical difficult and fruitful questions and even with Art. Renaissance artist studying polyhedra nearly discovered the Rhombic Dodecahedron. This interdisciplinary approach is an enriching way to study Mathematics and it appeals our students.
In this article we explore all these points of view and offer readers (and teachers, in particular) tested resources and materials that could be use to share the beauty of Mathematics. They can be adapted and used in the classroom or in workshops. These materials have different levels of difficulty, from building basic polyhedra to carrying out some calculations and even using derivatives to solve one more challenging optimization problem.
In this age of computers and electronic devices that gives us great opportunities of modeling, learning and sharing knowledge, perhaps we must highlight the interest of manual activities such as building polyhedra. Our students enjoy this kind of activity. We all like their aesthetic appeal but there is more: manipulating three-dimensional bodies we get a better understanding of the mathematical properties of these objects.
The study of the Rhombic Dodecahedron is perfect to achieve all these goals.
Caspar, Max. Kepler. Dover Publications, Inc., New York, 1993.
Coxeter, H.S.M. Introduction to Geometry. John Wiley and Sons, Inc, 1961. Chap. 10, pp.148-160, 'The Five Platonic Solids'.
Cromwell, Peter R. Polyhedra. Cambridge University Press, Cambridge, 1997.
Cundy, H.Martin and Rollet, A.P. Mathematical Models. Oxford University Press, Second Edition, 1961.
Fejes Tóth, L. What the bees know and what they do not know. Bull. Amer. Math. Soc. 70, 1964.
Heath,Thomas. A History of Grreek Mathematics. Volume II: From Aristarchus to Diophantus. Oxford University Press, 1921.
Field, J.V. Kepler's Geometrical Cosmology. Bloomsbury, 2013.
Hope-Jones, W. The Rhombic Dodecahedron for the Young. The Mathematical Gazette, 1936.
Kepler, Johannes. De Nive Sexangula (There is a Latin and English bilingual version 'The Six Cornered Snowflake: a New Year's gif'. Paul Dry Books, Philadelphia, Pennsylvania, 2010. Very interesting comments and notes by Owen Gingerich and Guillermo Bleichmar).
Kepler, Johannes. Harmonices Mundi. (The Harmony of the World) Translated into English with an Introduction and Notes by E.J.Aiton, A.M. Duncan, J.V.Field. American Philosophical Society, 1997.
Maclaurin, Colin. On the Bases of the Cells wherein the Bees deposite their Honey. 1743.
Luca Pacioli. La divina proporción. Ediciones Akal, 4th edition, 2004. Spanish translation by Juan Calatrava.
Pedoe, Dan. Geometry and the Liberal Arts. St. Martin's Press, New York, 1978.
Rouse Ball W.W. Mathematical Recreations & Essays. The MacMillan Company, 1947.
Steinhaus, Hugo. Mathematical Snapshots. Oxford University Press, 1983.
Szpiro, George G. Kepler's Conjecture. John Wiley and Sons, Inc. 2003.
Thompson, D'Arcy. On Growth And Form. Cambridge University Press, 1942.
Wenninger, Magnus. Polyhedron Models. Cambridge University Press, New York, 1971.

|
Kepler in Mac Tutor History of Mathematics
A biography of Kepler. |

|
Kepler: The Volume of a Wine Barrel
To learn more about Kepler contribution to the development of calculus we can read this article published in 'Convergence: Where Mathematics, History, and Teaching Interact'. |

|
Honeycomb: a property of minima
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?. |

|
Properties of the cuboctahedron.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube. We study some of its properties. This beautiful polyhedron is used as a decoration, in Art and jewelry. |

|
More about Kepler and cannonballs.
Centers of the twelve balls surrounding one central ball are vertices of a cuboctahedron. |
|
|
Trapezo-Rhombic Dodecahedron.
The Trapezo-Rhombic Dodecahedron has twelve faces but six of them are trapezoids. . |

|
Leonardo da Vinci: Drawing of an stellated octahedron (stella octangula) made to Luca Pacioli's De divina proportione.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula). |

|
Angles of the rhombic faces of a Rhombic Dodecahedron.
Maraldi |
|
|
Density of the optimal sphere packing.
Using the Rhombic dodecahedron as a unit cell it is not difficult to calculate the density of the optimal sphere packing. |
Roberto Cardil Ricol is a Secondary School teacher of Mathematics in Spain. He studied as a teacher (Huesca University, Spain), Bachelor in History (Barcelona University, Spain) and Bachelor in Mathematics (Zaragoza University, Spain). He has taught Mathematics to students from 6 years to the University. He maintains the site www.matematicasvisuales.com and enjoys the beauty of Mathematics.
I would like to thank Amy Ackerberg-Hastings and Janet Heine Barnett, Convergence editors, for their support, encouragement and good advice. Without their help this article would not have been published.
I thank the anonymous referees for suggestions that improved the article.
I am grateful to John Jeremiah Edminster for granting permission to use their designs of a rhombic box and a bee cell box. I am also grateful to Akal Editorial for granting permission for the use of images from the Pacioli's book 'La Divina Proporción'.
Miguel Cardil helped me in the artistic design of the page.