I am going to follow Serge Lang's exposition (A First Course in Calculus, p. 182-184).
After the definition of the logarithm function as an integral, and studying some of its
properties we can apply the theory of the inverse function. Since the function log
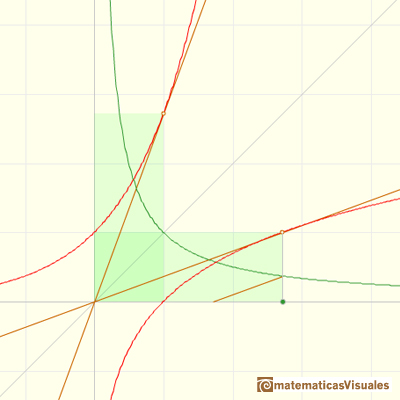
is strictly increasing, the inverse function is defined and we call it the Exponential (or antilogarithm) function, exp.
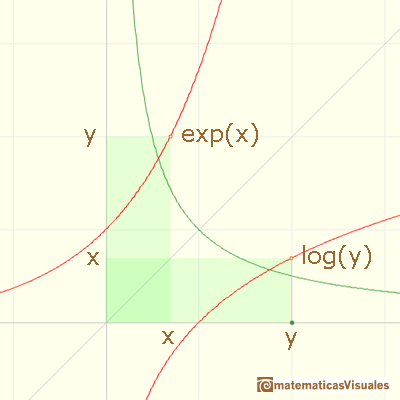
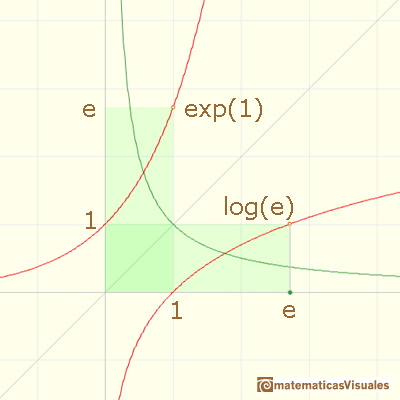
The graph of the exponential function is obtained from the graph of the logarithm by reflection through the diagonal line y=x.
Because for every real number x there is one and only one y such that log(y)=x then the domain of the exponential function is the entire real axis.
Since log and exp are inverses of each other, we have
Each property of the logarithm can be translated into a property of the exponential.
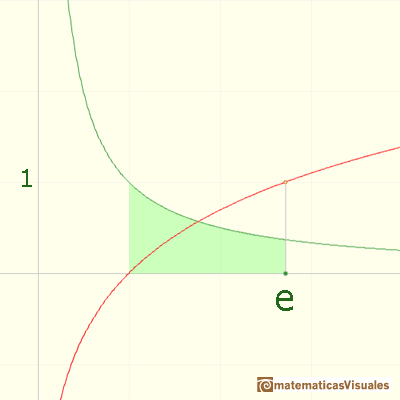
We can define the number e to be
If we remember the geometric interpretation of the log as the area under the curve 1/x, this means that
e is the number such that the area between 1 and e is equal to 1.
Using the property of the log it is not difficult to probe that
And now
By the theory of the derivatives of the inverse function, we know that the function exp es differentiable and
We define
We can rewrite (and see logarithms as exponents):
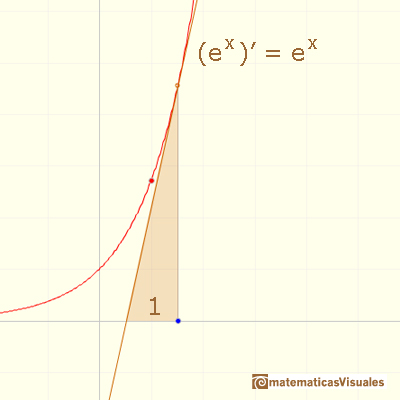
By definition, the derivative of exponential function is the limit of the quotient as h approaches 0.
Now we can obtain the limit
"This fact would have been very troublesome to obtain directly." (Serge Lang, p.184)
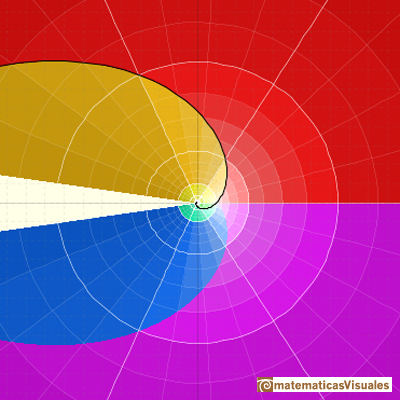
The Exponential function can be extended as a complex function.
You can generate colorful pictures that represent this complex function:
The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.
REFERENCES
A. I. Markushevich, Areas and Logarithms, D.C. Heath and Company, 1963.
Serge Lang, A First Course in Calculus, Third Edition, Addison-Wesley Publishing Company.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980.
MORE LINKS
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.
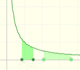
The natural logaritm can be defined using the integral of the rectangular hiperbola. In this page we are going to see an important property of this integral. Using this property you can justify that the logarithm of a product is the sum of the logarithms.
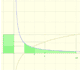
The main property of a logarithm function is that the logarithm of a product is the sum of the logarithms of the individual factors.
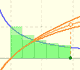
The logarithm of the number e is equal to 1. Using this definition of the number e we can approximate its value.
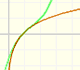
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.
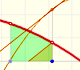
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
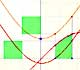
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
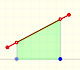
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
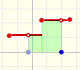
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
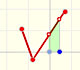
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
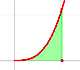
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
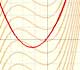
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
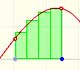
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.

Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

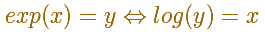

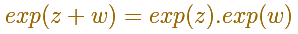
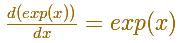
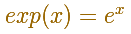
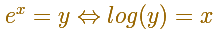
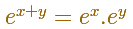
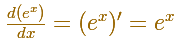
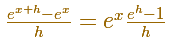

 NEXT
NEXT
 PREVIOUS
PREVIOUS