Power functions were the first class of functions to be integrated.
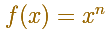
We need to calculate the area under the graph of a power function.
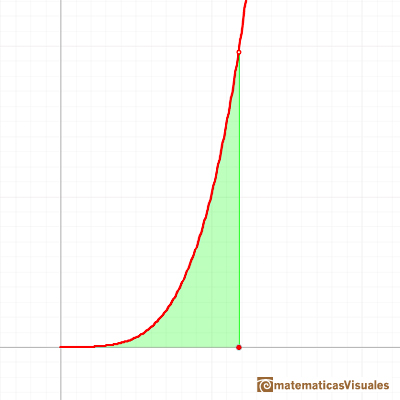
In modern notation the problem is


The problem was solved before the work of Newton and Leibniz, before mathematicians understood the relation between integration and derivatives. After the discovery of Calculus, and what now is called the Fundamental Theorem of Calculus, the answer is very easy and is a wonderful example of the power of these new tools in the simplest cases:
We are going to see some approaches to this problem before this powerful tool was known.
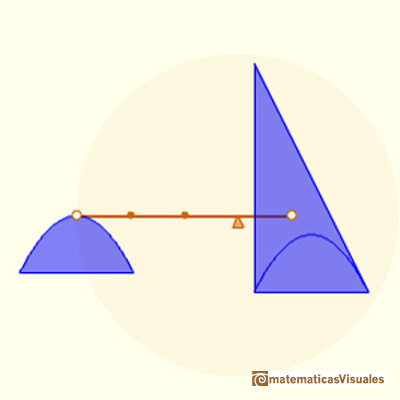
After the quadrature of the parabola by Archimedes (who died at 212 BC), Cavalieri (about 1630) was the first to succeed in an analogous problem. After Cavalieri, other mathematicians, like Torricelli, Roberval, Wallis and Fermat, worked and solved the problem completely.
The main idea followed by Archimedes, Cavalieri, Torricelli, Fermat and others (prior to Newton, Leibniz, Cauchy or Riemann, of course) is to divide the interval into thin rectangles and then the area is the sum of these thin rectangles.
Cavalieri divided the interval into equal parts, and he was able to succeed in cases as far as n=9. Wonderful achievement if we know the problems that he had to face. (Toeplitz pp. 52, Edwards pp. 106-113).
The quadrature of curves of the form y=xk, with k not necessarily a positive integer was first attacked systematically by John Wallis (1616-1703). Rational and negative exponents were introduced by him (1655). Wallis had a decisive influence on Newton's early mathematical development.
In this page we are going to follow how Fermat solved the problem for n a positive integer (this is the simplest cases and we are going to use modern notation). The same argument, with minor changes, works with n a positive rational number. Fermat was able to solve the problem for arbitrary n (except the important case n=-1) in one of his last papers. His Treatise on Quadrature (1659) appeared too late to have a profound effect on the development of calculus.
Fermat's idea was a very nice non trivial application of the sum of geometric series.
We need to remember how to sum a geometric series:
Later we are going to use the following polynomial factorization (you can see that it is related to the sum of a finite geometric progression):
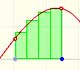
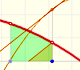
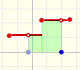
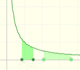
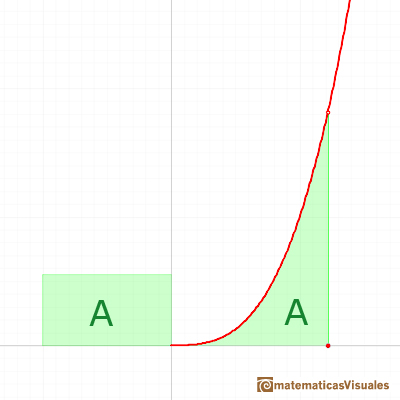
Fermat started dividing the interval of integration [0,a]. But not into equal subdivisions, but rather he used unequal subdivisions. His solution was to use a geometric progression to determine the width of this rectangles. The width of the rectangles increase in geometric progression.
Let be r a number between 0 and 1, then:
He considered rectangles with width:
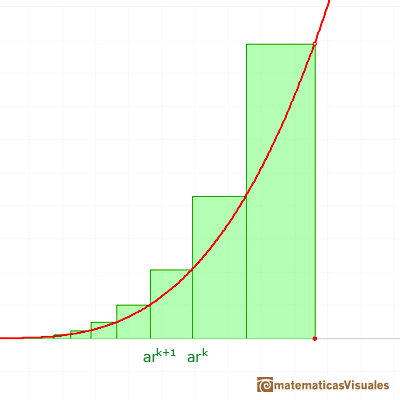
The width of these rectangles are in a geometric progression.
The height of each rectangle is:
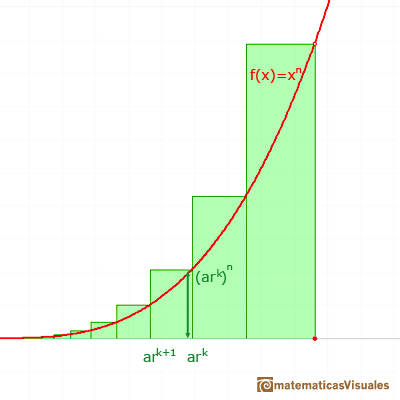
The area of each rectangle is:
These areas are in a geometric progression.
We can add up all these rectangles (the result depends on the value of r):

We know how to sum a geometric series:
Now we are going to use for the first time that n is a positive integer and we can simplify the expression:
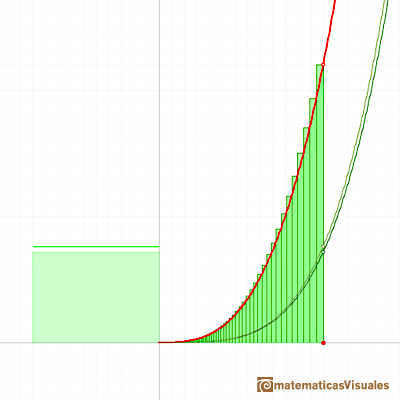
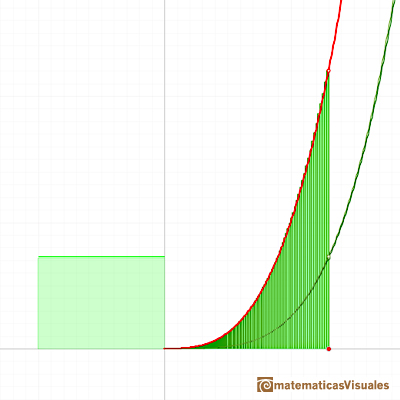
When the ratio r approaches 1 the denominator of this expression approaches n+1 and we can concluding with the result:
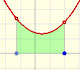
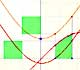
A very similar argument give us the integral of power functions with exponent the inverse of a positive integer:
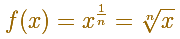
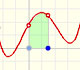
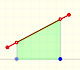
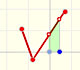
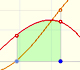
We can justify this case in a visual and intuitive way:
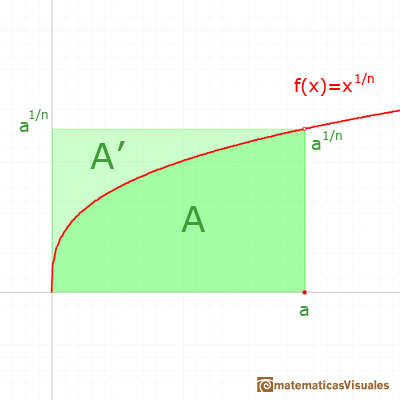
If you rotate the image, the function can be seen as xn and you know how to integrate this function, it is to say, we can calculate A'. It is very easy to calculate the area of the rectangle A+A', then it is easy to deduce A. You can try it!
With more generality, you can use geometric progressions to justify the case when the exponent is a positive rational (fractional powers) as Fermat did, it is to say, the function to integrate is:
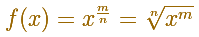
Fermat was able to integrate power functions with positive and negative exponent (except for the very important case of n=-1). This integral is related with the Logarithmic Function.
Boyer's point of view about Fermat: "In these quadratures we see most of the essential aspects of the definite integral - the division of the area under the curve into small elements of area, the approximate numerical determination of the sum of these by means of rectangles and the analytic equation of the curve, and finally an attempt by Fermat of express the equivalent of what we would call the limit of this sum, as the number of elements is indefinitely increased and as the area of each becomes indefinitely small. One is almost tempted to say that Fermat recognized all the aspects except that of the integral itself; that is, he did not recognize the operation involved as significant in itself. The procedure was for him, as it has been for all of his predecessors, simply that of finding a quadrature -of answering a specific geometrical question. Only with Newton and Leibniz were the processes involved in infinitesimal consideration recognized as constituting operations, independent of any geometrical or physical considerations, to which characteristic names were applied." (Boyer, pp.161-162)
Edwards' Summary: "During the middle decades of the seventeenth century infinitesimal techniques or indivisibles, motivated by attempts to relax the rigor of the classical method of exhaustion, wre applied to establish the basic quadrature result
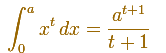
It was this result itself, rather than the particular methods used to derive it, that was of lasting importance. For by 1660 the early direct methods of quadrature were rapidly approaching obsolescence, soon to be superseded by indirect methods based on the interplay between quadrature and tangent methods." (Edwards, pp. 120-121)
Archimedes, Cavalieri, Fermat, Torricelli, Wallis and others worked wery hard to integrate power functions. But these integrals are very easy to solve after the discoveries of Newton and Lebiniz (as an application of what nowdays is known as the Fundamental Theorem of Calculus).
REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS