Two points with different values of x determine a linear function (a polynomial of degree less or equal to 1)

The derivative of a lineal function is a constant function.
Three points not in a line determine a parabola, a polynomial function of degree 2.
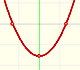
Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.
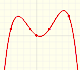
Then four points not in a line nor in a parabola determine a cubic function.
A cubic function is a polynomial function of degree 3. Cubic functions have the expression:
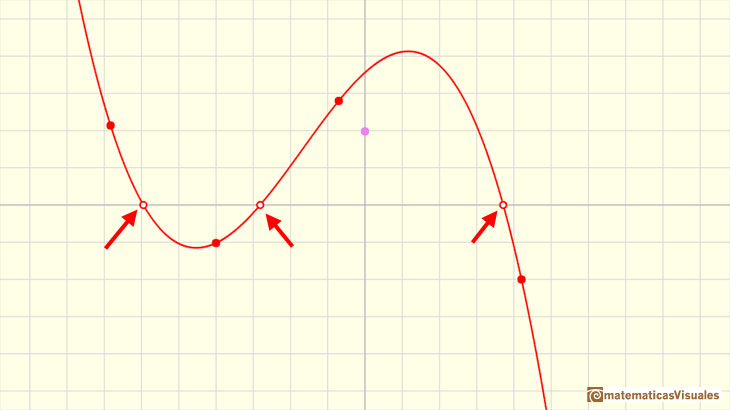
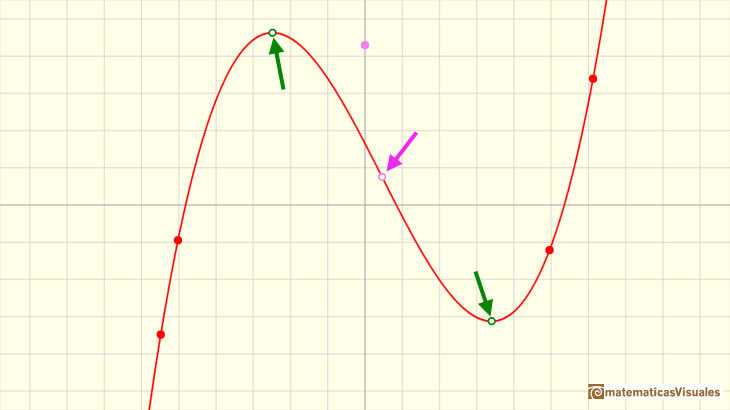
A cubic function can have three different real roots:
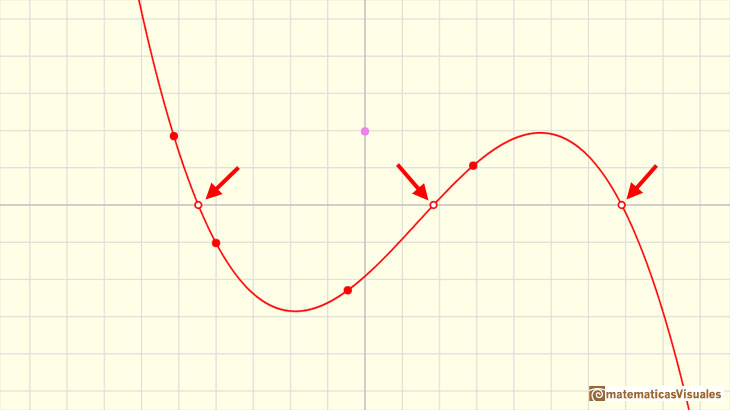
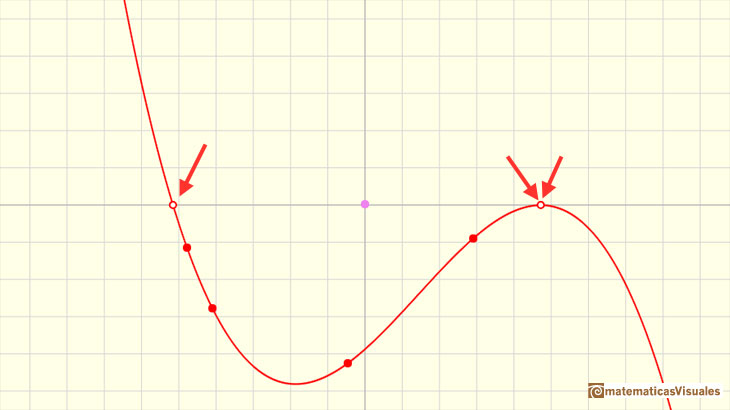
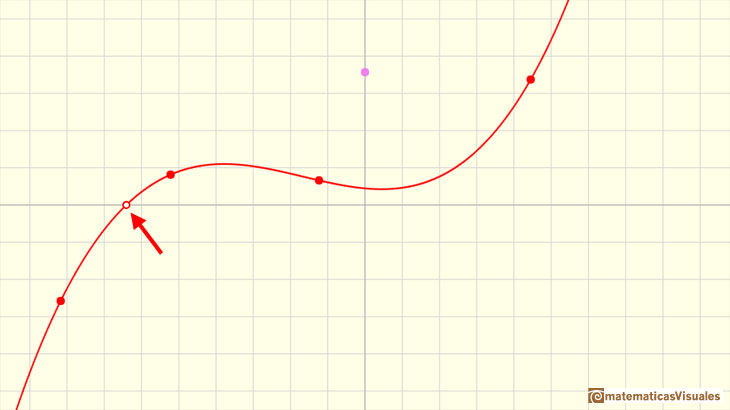
It can have two different real roots (one of these is a double root):
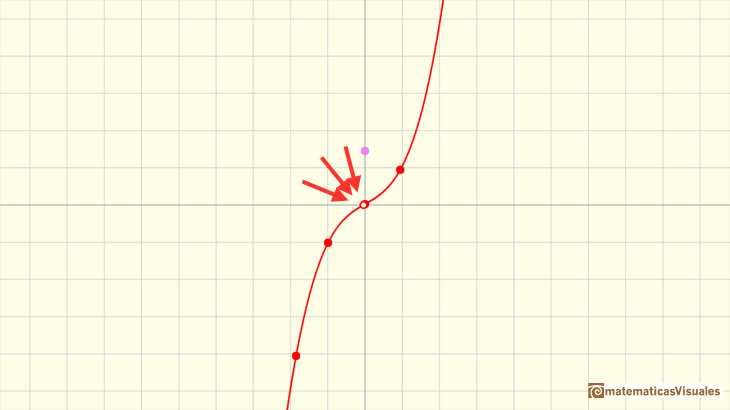
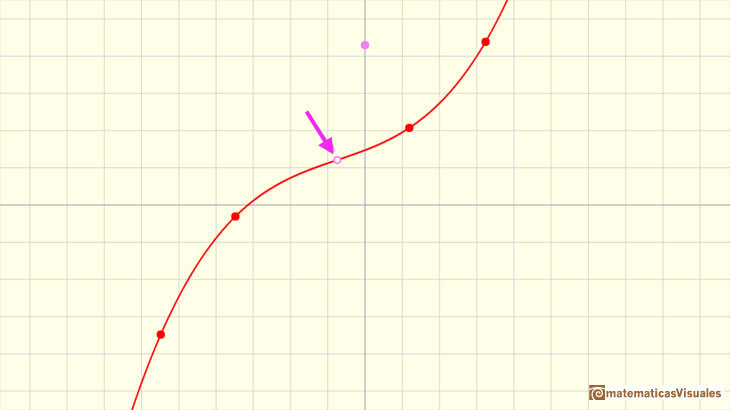
A cubic function can have one one real root (a triple root), for example f(x)= x^3
Some cubic function only have one real root (and two complex conjugate roots):
INVESTIGATE
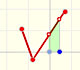
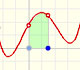
Clicking in the checkbox 'Zeros' you can see the zeros of a cubic function. Playing with the red points or translating the graph vertically moving the violet
dot you can see how the zeros mix together in a double zero or in a triple zero.
All cubic functions (or cubic polynomials) have at least one real zero (also called 'root'). This is a consequence of the Bolzano's Theorem or the
Fundamental Theorem of Algebra.
INVESTIGATE
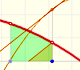
A cubic function always has a special point called inflection point.
Some cubic functions have one local maximum and one local minimum. In this case, the inflection point of a cubic function is 'in the middle'
Clicking the checkbox 'Aux' you can see the inflection point. Changing the points you can see that sometimes the maximum and the minimum mix together in
the inflection point.
REFERENCES
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
I.M. Gelfand, E.G. Glagoleva, E.E. Shnol, 'Functions and Graphs', Dover Publications, Mineola, N.Y.
MORE LINKS
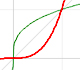
Power with natural exponents are simple and important functions. Their inverse functions are power with rational exponents (a radical or a nth root)
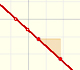
Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.

The derivative of a lineal function is a constant function.
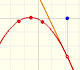
The derivative of a quadratic function is a linear function, it is to say, a straight line.
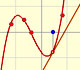
The derivative of a cubic function is a quadratic function, a parabola.
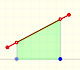
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
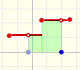
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
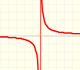
Rational functions can be writen as the quotient of two polynomials. Linear rational functions are the simplest of this kind of functions.
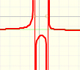
When the denominator of a rational function has degree 2 the function can have two, one or none real singularities.
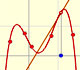
Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
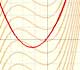
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.

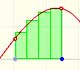
Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
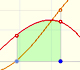
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.

It is easy to calculate the area under a straight line. This is the first example of integration that allows us to understand the idea and to introduce several basic concepts: integral as area, limits of integration, positive and negative areas.
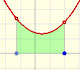
To calculate the area under a parabola is more difficult than to calculate the area under a linear function. We show how to approximate this area using rectangles and that the integral function of a polynomial of degree 2 is a polynomial of degree 3.
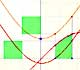
We can see some basic concepts about integration applied to a general polynomial function. Integral functions of polynomial functions are polynomial functions with one degree more than the original function.
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).

By increasing the degree, Taylor polynomial approximates the exponential function more and more.
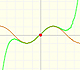
By increasing the degree, Taylor polynomial approximates the sine function more and more.
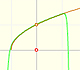
The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
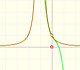
The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
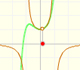
This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.
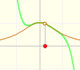
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.


 NEXT
NEXT
 PREVIOUS
PREVIOUS