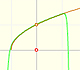
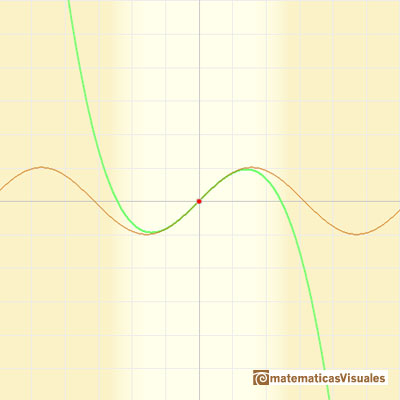
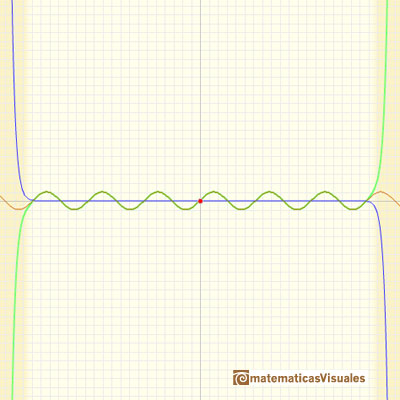
As in the case of the Exponential function, the parabolas give usable approximations to the original curve for a greater and greater interval. The parabolas make the effort to share more and more oscillations with the sine curve. (Felix Klein)

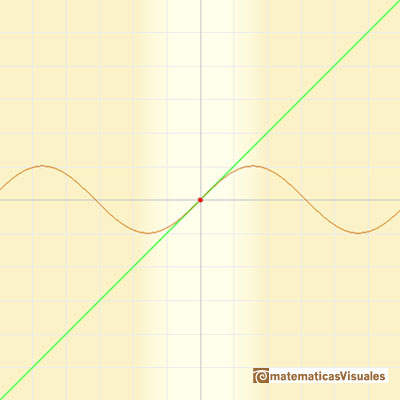
Taylor's series of the sine function at x=0 is:

We say that the sine function is an odd function because in this power series (and in the Taylor's polynomials centered at the origin) the only terms are those with odd exponent.

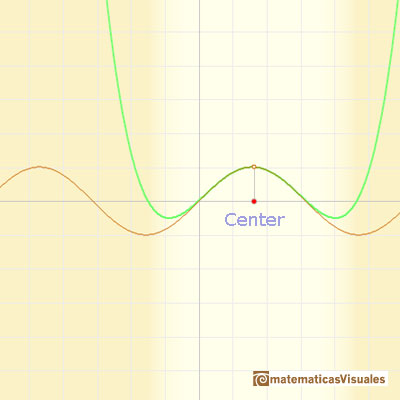
We can change the center and see that the behavior of the approximation is equally good.

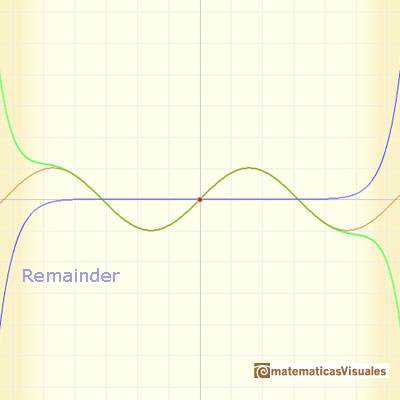
The behavior of these power series is very good. We say then that the infinite series for the sine function converge for all values of x.

It can't be the case for all functions. For example, what happens if some values aren't in the Domain of a function?. We can study one simple example: Taylor polynomials (3): Square root.

REFERENCES

MORE LINKS

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

Taylor polynomials (4): Rational function 1

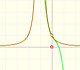
The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (6): Rational function with two real singularities

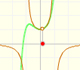
This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.

Taylor polynomials (7): Rational function without real singularities

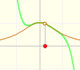
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Mercator and Euler: Logarithm Function

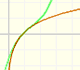
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

The Complex Cosine Function

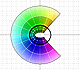
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function: mapping an horizontal line

The Complex Cosine Function maps horizontal lines to confocal ellipses.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

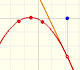
The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

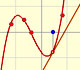
The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.