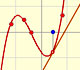
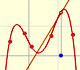
Taylor polynomials: Rational function 1
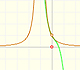
The rational function

is, as in the example of the square root, a special case of Newton's Binomial Theorem. We can calculate its Taylor's series at x = 0 easily.
This function has a singularity at the point x =- 1. The approximation is good in ranges from -1 to +1. Again we find a useful approach that is centered on the origin.

At the point x = +1 their ordinates are alternately equal to 1 and 0, while that of the original curve has the value 1/2.

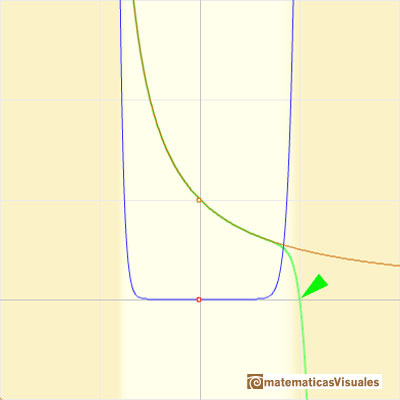
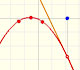
We can compare this behavior with that of the rational function 2.
REFERENCES
Felix Klein - Elementary Mathematics from an Advanced Standpoint. Arithmetic, Algebra, Analysis (pags. 223-228) - Dover Publications
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS
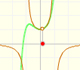
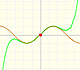
This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.
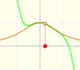
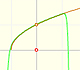
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.
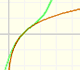
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.