|
|
En casa: Actualizaciones
1 de Junio de 2020
Despedida del proyecto 'matemáticasVisuales En casa': el enanito que desaparece
 |
Conocido rompecabezas en el que al cambiar dos piezas de un dibujo desaparece uno de los enanitos. ¿Qué explicación tiene?.
|
27 de Mayo de 2020
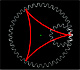 |
Generación mediante engranajes de varias curvas de la familia de las hipocicloides: astroide, deltoide y otras.
|
 |
Más ejemplos de curvas de la familia de las hipocicloides generadas mediante engranajes.
|
 |
Generación mediante engranajes de varias curvas de la familia de las epicicloides: cardiode, nefroide y otras.
|
25 de Mayo de 2020
Cicloide y epicicloides
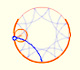 |
Se presenta la cicloide y se muestra una deformación continua de la cicloide en otras hipocicloides como la deltoide.
|
22 de Mayo de 2020
 |
Las torres de Hanoi es un rompecabezas que aquí se presenta haciendo una versión sobre un cuadro de Magritte.
|
20 de Mayo de 2020
Volumen del tetraedro
 |
Construcción con pajitas de refresco de un octaedro al que se le añaden cuatro tetraedros para obtener un tetraedro grande.
|
 |
Añadiendo cuatro tetraedros a un octaedro podemos obtener un tetraedro. Calculamos el volumen de un tetraedro a partir del volumen de un octaedro y usando semejanza.
|
18 de Mayo de 2020
Un tetraedro en un cubo
 |
Una manera muy elegante de dar rigidez al cubo es construir un tetraedro dentro del cubo. A partir de un cubo se pueden construir dos tetradros distintos de este modo.
|
 |
Estudiamos algunas medidas de la construcción de un tetraedro en un cubo. Calculamos el volumen del cubo a partir de la arista del tetraedro.
|
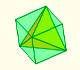 |
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.
|
15 de Mayo de 2020
Circunferencias
 |
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por dos puntos.
|
 |
Animación inspirada en el trabajo de Jean Louis Nicolet y Caleb Gattegno sobre circunferencias que pasan por tres puntos.
|
13 de Mayo de 2020
Circunferencias y círculos
 |
Todas las circunferencias son semejantes. Esta idea tan simple nos lleva a un concepto muy importante, la definición del número Pi.
|
 |
Una aproximación intuitiva al área de un círculo. Para calcular el área de un círculo también necesitamos el número Pi.
|
11 de Mayo de 2020
Origami para los más pequeños
 |
Plegado y decoración de una piraña de origami. Figura muy sencilla para introducir a los más pequeños en el origami. A un paso de hacer la pajarita.
|
8 de Mayo de 2020
Rectángulos áureos
 |
Los rectángulos áureos están relacionados con los pentágonos regulares. Exploramos alguna propiedad de estos rectángulos.
|
 |
La propiedad de los rectángulos áureos nos lleva a un interesante proceso infinito.
|
 |
Partiendo de un rectángulo áureo podemos dibujar la preciosa y sencilla espiral de Durero.
|
6 de Mayo de 2020
Rectángulos
 |
No todos los rectángulos son semejantes pues tienen distintas formas, unos son más alargados que otros.
|
 |
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
|
 |
Calculamos la relación entre el largo y el ancho de una hoja de papel Din A4.
|
5 de Mayo de 2020
Más ejercicios sobre áreas y volúmenes
 |
Construcción de una piscina de cartulina a escala. Haremos algunos cálculos a partir de esa construcción.
|
 |
Ejercicio sobre el volumen y peso de la cabeza de un martillo.
|
4 de Mayo de 2020
Origami modular
 |
Plegado de un tetraedro usando dos módulos de origami. Se propone la construcción de un cubo de cartulina en el que cabe nuestro tetraedro.
|
3 de Mayo de 2020
Datos de visitas a matemáticasVisuales
 |
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.
|
2 de Mayo de 2020
El pentágono
 |
La diagonal y el lado de un pentágono regular están en proporción áurea. Utilizando semejanza llegaremos a calcular el valor de la razón áurea.
|
 |
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
|
28 de Abril de 2020
Funciones racionales
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
 |
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
|
27 de Abril de 2020
Ángulos
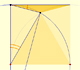 |
Se propone una construcción con regla y compás y probar la medida de un ángulo del dibujo.
|
26 de Abril de 2020
Magia
 |
Propuesta de dibujar unas tarjetas para hacer un truco de magia apto para los más jóvenes. Con ellas adivinaremos el pensamiento. El fundamento matemático es muy interesasnte.
|
25 de Abril de 2020
Ángulos
 |
Si doblamos un cuadrado de papel por la mitad obtenemos un triángulo. ¿Qué ángulos se han formado? ¿Cómo es el triángulo?.
|
 |
Con unos sencillos pliegues podemos doblar un triángulo equilátero. ¿Sabrías demostrar que los ángulos son de 30º y de 60º?.
|
23 de Abril de 2020
Funciones polinómicas que dependen de un parámetro
 |
Representación de una familia de funciones afines que dependen de un parámetro.
|
 |
Representación de una familia de funciones afines que dependen de un parámetro.
|
 |
Representación de una familia de funciones afines que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
 |
Representación de una familia de funciones cuadráticas que dependen de un parámetro.
|
21 de Abril de 2020
Más ejercicios de la Primavera Matemática de nivel 1
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
20 de Abril de 2020
 |
Técnica sencilla para construir poliedros pegando discos de cartulina o de cartón de caja de galletas. Se propone la construcción de un icosaedro.
|
18 de Abril de 2020
Análisis. Continuidad de funciones
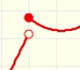 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Una de las funciones es afín y la otra es quadrática.
|
 |
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Una de las funciones es afín y la otra es quadrática.
|
17 de Abril de 2020
 |
Dibujo del desarrollo de una casita a escala. Haremos algunos cálculos a partir de esa construcción.
|
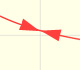 |
Estudio del concepto de continuidad de una función desde un punto de vista intuitivo. Algunos tipos de discontinuidades.
|
16 de Abril de 2020
 |
Proponemos hacer esta famosa construcción del esqueleto de un icosaedro formado por tres rectángulos áureos usando el cartón de una caja de leche.
|
15 de Abril de 2020
 |
Podemos construir un cuadrado doblando y cortando un folio. Se trata de un ejercicio muy básico de origami. Mediremos la diagonal.
|
 |
Podemos construir un cuadrado con pajitas de refresco. Notamos que no es rígido. Si lo deformamos obtenemos rombos. Para conseguir que sea rígido podemos añadir una pajita en la diagonal.
|
14 de Abril de 2020
Homenaje a John Conway: el Juego de la Vida
 |
El Juego de la Vida, inventado por John H. Conway, es uno de los autómatas celulares bidimensionales más famosos.
|
13 de Abril de 2020
 |
Construcción de una sección rómbica del cubo con pajitas de refresco. Hacemos unos cálculos sobre esa sección.
|
11 de Abril de 2020
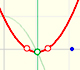 |
Estudio y clasificación de una familia polinómica de grado 2 que depende de un parámetro. Sus dos raíces pueden ser las dos reales y distintas, una raíz real doble o dos raíces complejas conjugadas.
|
 |
Estudio de las raíces reales o complejas de una familia polinómica de grado 2 que depende de un parámetro. Representación gráfica en el plano complejo.
|
8 de Abril de 2020
 |
Actividad de origami tradicional, muy sencilla de hacer y muy bonita. Nos introduce en el conocimiento del pentágono y sus diagonales.
|
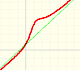 |
Para valores grandes en valor absoluto de la variable x algunas funciones se comportan como una recta oblicua. A esta recta la llamamos asíntota oblicua de la función.
|
7 de Abril de 2020
 |
Vamos a calcular la diagonal de un cuadrado. Para presentar la idea usaremos el lenguaje de las funciones.
|
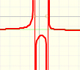 |
Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).
|
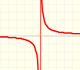 |
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
|
6 de Abril de 2020
Nueva sección de En casa: Actualizaciones
 |
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
|
 |
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal de un modo intuitivo.
|
 |
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal usando el lenguaje de las funciones.
|
 |
Si colocamos una diagonal en nuestro cuadrado conseguimos darle rigidez. Calculamos la diagonal usando el teorema de Pitágoras.
|
3 de Abril de 2020
Nueva sección de En casa: cálculo mental
 |
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
|
 |
Construcción de un tetraedro con un rollo de papel higiénico. Esta técnica se usó y todavía se usa para envasar productos.
|
2 de Abril de 2020
 |
Construcción de los cinco sólidos platónicos con pajitas de refresco. Contamos sus elementos (sus caras, aristas y vértices) y vemos si son rígidos o no.
|
 |
Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
1 de Abril de 2020
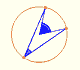 |
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
|
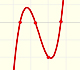 |
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
31 de Marzo de 2020
 |
Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
|
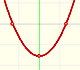 |
Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
30 de Marzo de 2020
Se inicia la publicación de matemáticasVisuales.En casa
 |
Página con enlaces de actividades matemáticas que podemos hacer en casa.
|
 |
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
|
 |
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
|
 |
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
|
 |
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
|
 |
Construcción de un octaedro con ocho cuadrados de papel. Los seis vértices del octaedro están en 3 cuadrados.
|
 |
Construcción de un cubo con cartulina. Dentro de él podemos poner un octaedro de origami. Una idea interesante asociada a esta construcción es la dualidad de cubo y octaedro.
|
 |
Presentación de los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro.
|
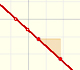 |
Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.
|
|




































































