Las funciones más simples son las funciones afines. Sus fórmulas son polinomios de grado uno o cero (este es el caso
de la función constante). Sus gráficas son líneas rectas.
Una fórmula de estas funciones afines es:
Esta es la expresión explícita de una recta, donde b es la ordenada en el origen y m es la pendiente.
La pendiente, también llamada gradiente de la recta, mide la inclinación de la línea con la horizontal, el eje X.
La pendiente de una recta caracteriza la dirección hacia la que apunta la recta.
Cuando la pendiente, m, es positiva, la recta es creciente (hacia la derecha va hacia arriba). Cuanto mayor es m más hacia arriba se dirige
la recta.
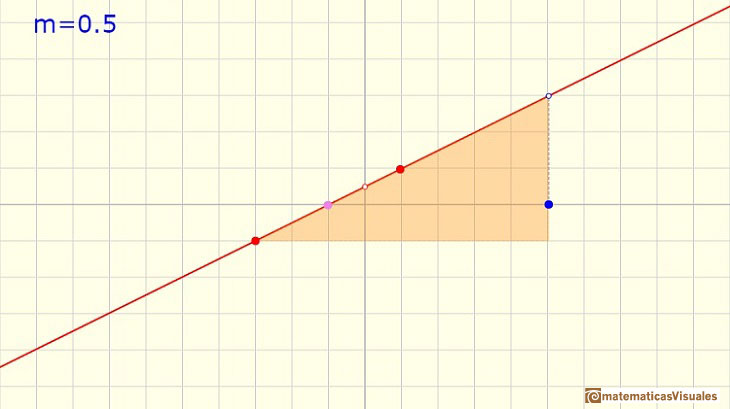
Cuando la pendiente es negativa la línea es decreciente (hacia la derecha va hacia abajo).
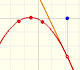
Este es un ejemplo de una función afín con pendiente negativa:
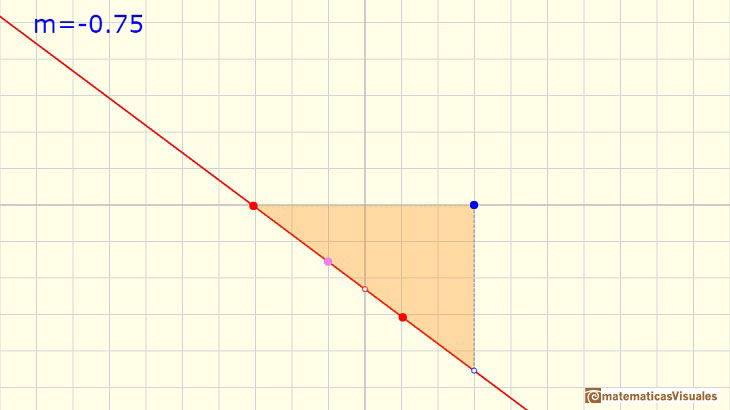
Las rectas horizontales tienen pendiente m=0. Todas las rectas horizontales son de la forma y = k (donde k es un número real).
Como funciones, son las funciones constantes.
Las rectas verticales no tienen pendiente. No son funciones. Si tratamos de calcular la pendiente estamos dividiendo entre 0.
El punto de corte con el eje de ordenadas es el punto donde el gráfico de la función cruza al eje Y (eje de ordenadas).
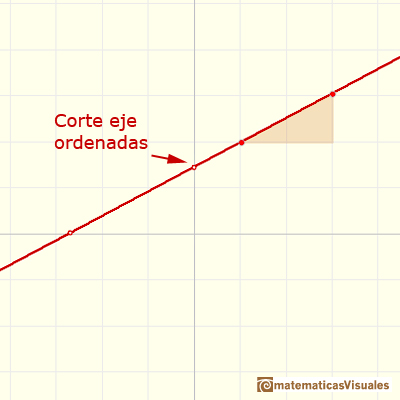
Cuando b es positivo, la recta corta al eje de ordenadas por encima del eje X (y=0) y si b es negativo, la línea cruza al eje de
ordenadas por debajo del eje X.
Una recta está completamente determinada por dos puntos distintos de esa recta.
Si
(x0, y0) y
(x1, y1) son dos puntos (x0 distinto de x1) de una recta podemos calcular la pendiente
de la recta:
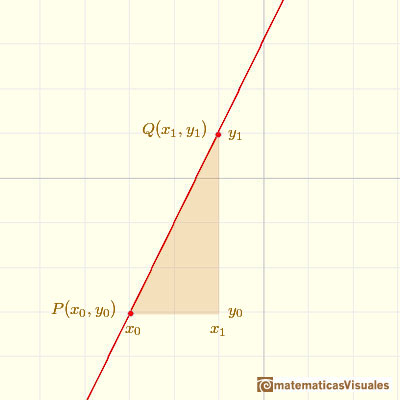
En aplicaciones, si conocemos que una relación funcional entre variables se caracteriza por una razón de cambio constante, entonces
la función es afín y la pendiente mide esa razón de cambio. Usamos esta información para escribir la fórmula de la función.
La línea que pasa por P(x0, y0) con pendiente m se puede expresar así: (forma punto-pendiente):
Podemos reordenarla para escribir esta expresión como una función:
Podemos escribir la ecuación de la recta que pasa por dos puntos:
Tiene la ventaja de que no tenemos que dividir. Podemos llegar a la forma general (esta forma algebraica tiene la ventaja de que incluye
rectas verticales x = k, donde k es cualquier número real):
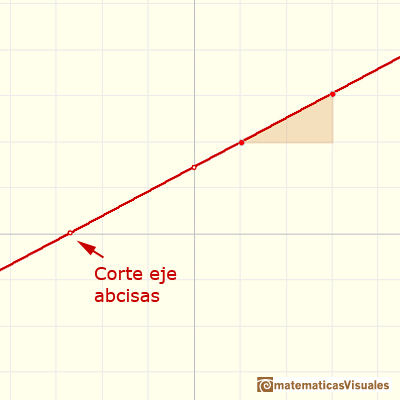
Un valor importante es el punto en el que la gráfica de la recta corta al eje de las Xs (eje de abcisas). Todas las rectas que no sean horizontales
tienen un punto de corte con el eje de abcisas. Para calcularlo resolvemos la ecuación:
La solución de la ecuación se llama raíz del polinomio. Más adelante veremos que, en general, una función puede tener varios de estos valores de
corte con el eje de abcisas.
El valor de x para el que la función lineal (con pendiente m distinta de 0) es:
El ejemplo más simple de Polinomio de Lagrange es, desde luego, la función afín a través de dos puntos. Podemos escribir esta función
afín como un ejemplo básico de Polinomio de Lagrange:
MÁS ENLACES
Potencias con exponente natural son funciones importantes pues son la base de los polinomios. Sus funciones inversas son las raíces que son funciones potencia con exponente racional positivo.
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.
Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.
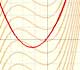
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.
La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.
Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.
Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.
Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.
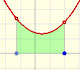
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
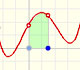
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.
El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.
El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
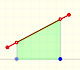
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
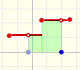
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
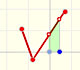
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
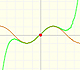
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
Las potencias de exponente natural tienen un cero de multiplicidad n.
Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.
Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.
Un polinomio de grado n tiene n ceros o raíces.
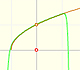
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
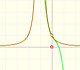
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
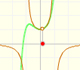
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.
SIGUIENTE
