Félix Klein empieza su capítulo dedicado al Teorema de Taylor "trayendo al primer plano las series finitas, tan importantes el la práctica, y ayudando a la visión intuitiva de la situación con gráficos. De esta manera pareceran elementales y fácilmente comprensibles."

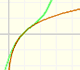
"Empezamos con la cuestión de si se pueden hacer approximaciones adecuadas a una curva arbitraria y = f(x), aunque sea sólo una parte, por medio de curvas del tipo más sencillo." (Klein, 'Elementary Mathematics from an Advanced Standpoint' p.223)

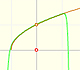
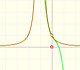
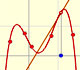
Podemos hacer estas aproximaciones usando polinomios de grado cada vez mayor, comenzando por la recta tangente a la función en un punto.

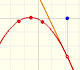
Podemos obtener mejores aproximaciones usando parábolas de segundo, tercer, ... orden.

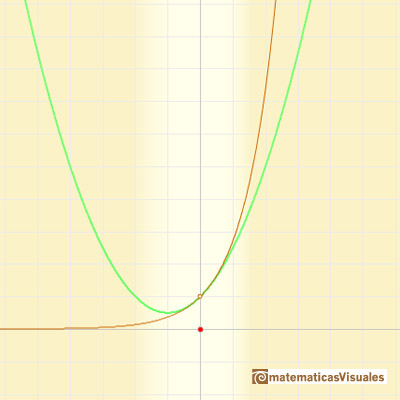
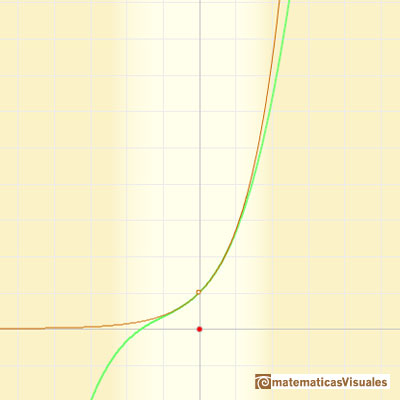
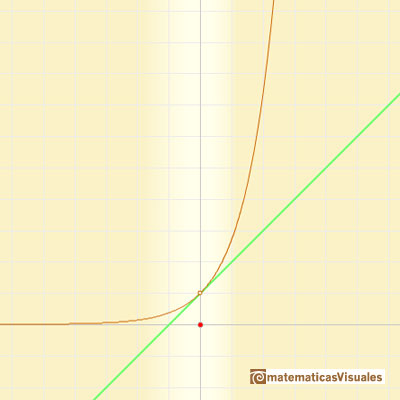
Son fáciles de calcular y aproximan a la curva alrededor de un punto (llamamos a estos polinomios 'parábolas osculatrices' porque están cerca de la curva tanto como es posible) "Entonces la parábola de orden 2 coincidirá con y=f(x) no sólo in su ordenada sino también en su primera y segunda derivadas (es decir, 'osculará'). (Klein, p. 224) Estos polinomios se conocen como Polinomios de Taylor y se obtienen considerando los primeros terminos de la serie de Taylor (esencialmente, derivando sucesivamente la función)

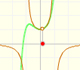
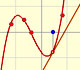
Tenemos que investigar cómo estos polinomios representan curvas de aproximación útiles y, en particular, en qué zona son precisas.

"La primera cuestión es muy importante en la práctica es cómo de próxima está la n-ésima parábola de osculación de la curva original. Esto implica estimar el resto de los valores de la ordenada, y esto está conectado naturalmente con el paso de n al infinito. ¿Puede ser representada la curva, al menos en una parte, por una serie de potencias infinita?" (Klein, p. 226) (Klein, p. 226)

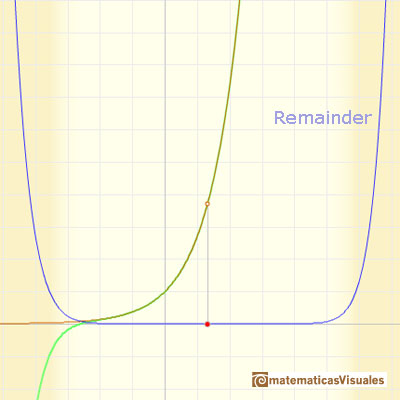
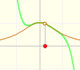
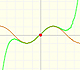
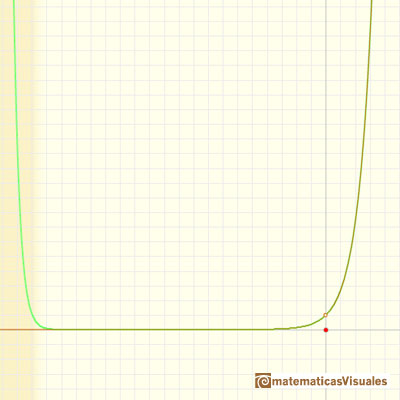
En el caso de la función exponencial, conforme incrementamos el grado, las parábolas nos dan aproximaciones precisas de la curva original en un intervalo cada vez mayor. Es un comportamiento muy bueno. Decimos entonces que la serie infinita converge para todos los valores de x.

Otras funciones se comportan igual, por ejemplo, Polinomios de Taylor (2): función seno. Pero no es siempre el caso. Desde luego, para las funciones que no son continuas, los polinomios de Taylor no pueden comportarse así pero veremos que incluso con algunas funciones continuas el comportamiento es misterioso.

La serie de Taylor de la función exponencial en x = 0 es:

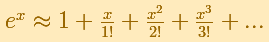
Para entender mejor estas series de potencias debemos investigar el plano complejo, por ejemplo, Polinomios de Taylor: Función Exponencial Compleja.

REFERENCIAS

MÁS ENLACES

Polinomios de Taylor: función exponencial compleja

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

Polinomios de Taylor (3): raíz cuadrada

La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (4): función racional 1

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (5): función racional 2

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (6): función racional con 2 singularidades

La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.

Polinomios de Taylor (7): función racional sin singularidades reales

La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Mercator y Euler: La función logaritmo

Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

Función exponencial compleja

La función exponencial compleja extiende la función exponencial real al plano complejo.

Funciones polinómicas y derivada (1): Funciones afines

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

Funciones polinómicas y derivada (2): Funciones cuadráticas

La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

Funciones polinómicas y derivada (3): Funciones cúbicas

La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

Funciones polinómicas y derivada (4): Polinomios de Lagrange (funciones polinómicas en general)

Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.