matematicasVisuales |Probabilidad

Probabilidad

Variables aleatorias
	Distribución binomial La distribución binomial modela una situación en la que hay n ensayos independientes con una probabilidad constante de éxito.
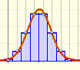	Aproximación normal a la distribución Binomial En algunos casos, una distribución Binomial puede aproximarse con una distribución Normal con la misma media y varianza.
	Distribución de Poisson La distribución de Poisson también se llama distribución de sucesos raros.
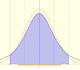
	Distribución Normal Las distribucines normales fueron estudiadas por Gauss. Son variables aleatorias continuas (la variable puede tomar cualquier valor real). La función de densidad tiene forma de campana.
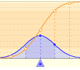	Distribuciones normales: Una, dos y tres desviaciones típicas Una propiedad importante de las distribuciones normales es que si consideramos intervalos centrados en la media y con una longitud proporcional a la desviación típica, la probabilidad de estos intervalos es constante independientemente de la distribución normal considerada.
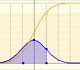	Distribuciones Normales: Función de Distribución (acumulada) La función de distribución (acumulada) de una variable aleatoria X, evaluada en x, es la probabilidad de que X tome valores menores o iguales que x. En esta página estudiamos las distribuciones normales.
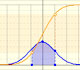	Distribuciones Normales: Probabilidades de intervalos simétricos Calculamos probabilidades de intervalos simétricos en torno a la media en distribuciones normales.
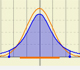
	Distribución t de Student La distribución t de Student fue estudiada por Gosset y se aproxima a una distribución normal.
	Cálculo de probabilidades en distribuciones t de Student