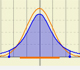
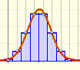
La función de distribución (acumulada) de una variable aleatoria X, evaluada en x, es la probabilidad de que X tome un valor menor o igual que x. La palabra 'acumulada' es redundante y se puede omitir.
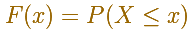
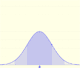
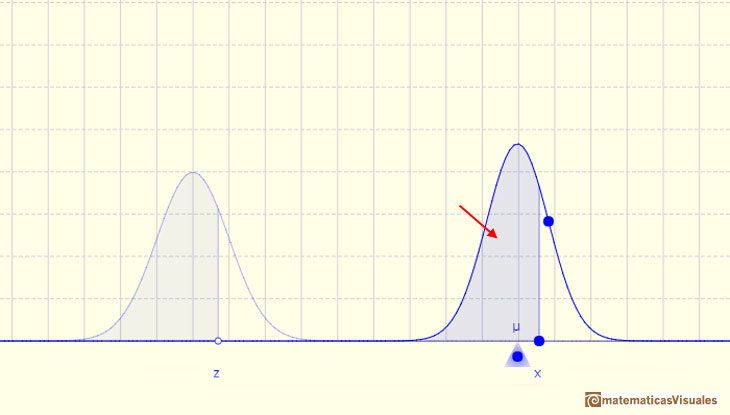
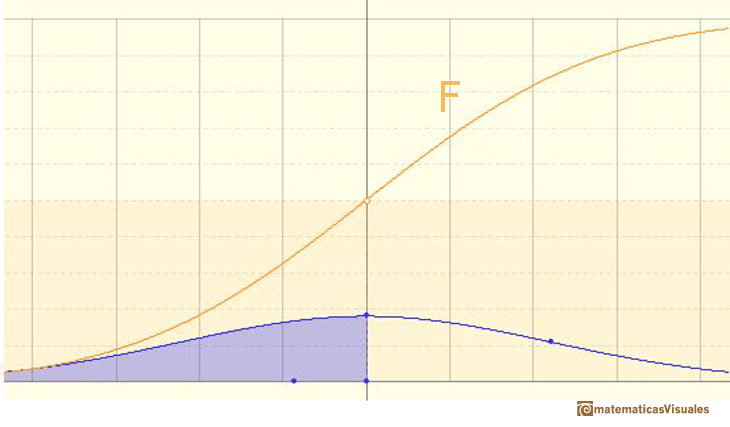
En el caso de que la distribución sea continua (como en las distribuciones normales) es el área bajo la función de densidad (la 'campana' que, a veces, llamamos 'campana de Gauss') desde menos infinito hasta x. La zona señalada en azul en la curva representa la probabilidd de que X sea menor o igual que x.
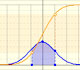
La función de distribución F es siempre no decreciente. En nuestro caso es estrictamente creciente y continua. Tiene forma de 'S'.
Si usamos la notación integral, entonces la función de distribución puede escribirse como una integral de su función de densidad:
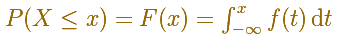
En el caso de las distribuciones normales esta integral no tiene una fórmula explícita. Se tiene que calcular numéricamente.
La distribución normal estándar juega un papel importante
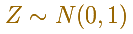
En algunos libros se suele usar una notación especial para la función de distribución en el caso de la distribución normal estándar:
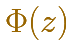
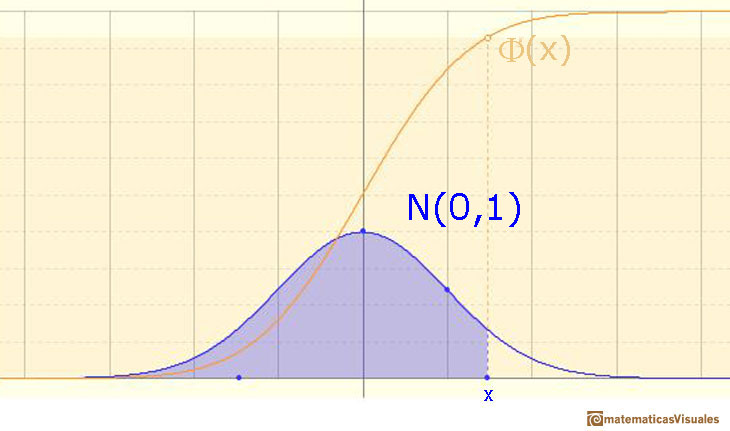
Ya sabemos que hay una relación entre cualquier distribución normal X y la distribución normal estándar Z que tiene media 0 y desviación estándar 1.
Este resultado es mucho más general: Cualquier distribución normal arbitraria X se puede transformar en una distribución normal estándar Z usando un cambio de variable
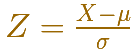
Lo que hacemos es que la media y la varianza de la variable aleatoria sean 0 y 1, respectivamente.
A esto se le llama estandarizar o tipificar la distribución normal. Cualquier valor de una distribución normal puede transformarse en su correspondiente valor en la distribución normal estándar. Para estandarizar un valor lo que hacemos es restar la media y dividir por la desviación estándar.
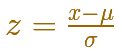
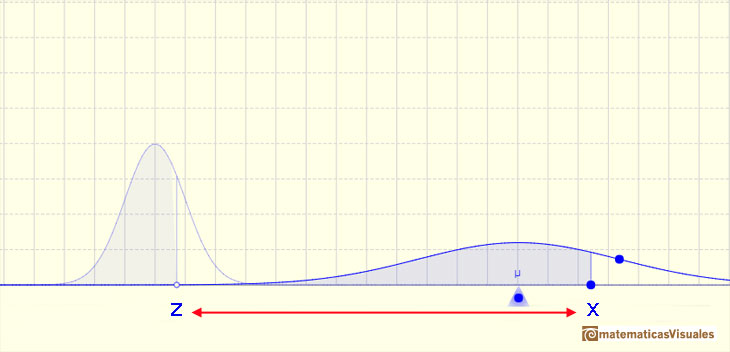
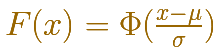
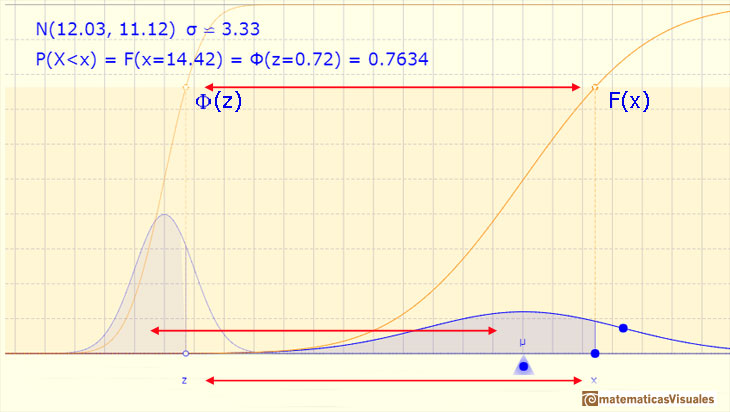
Este hecho tiene consecuencias prácticas importantes. Sabemos que las distribuciones normales son una familia infinita de distribuciones y que para calcular probabilidades necesitamos calcular una integral y que esto sólo lo podemos hacer numéricamente. Lo que nos dice el resultado es que sólo necesitamos una tabla de datos o sólo una función principal programada en cualquier lenguaje (si estamos usando ordenadores). Necesitamos conocer la integral de la distribución normal estándar (y no infinitas tablas para cada una de las infinitas distribuciones normales posibles).
Con la función de distribución podemos calcular la probabilidad de cualquier intervalo:
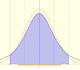
La probabilidad de que una variable aleatoria esté en un rango determinado se corresponde con el área bajo la función de densidad en ese intervalo. Para hacer estos cálculos usamos la función de distribución.
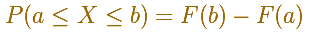
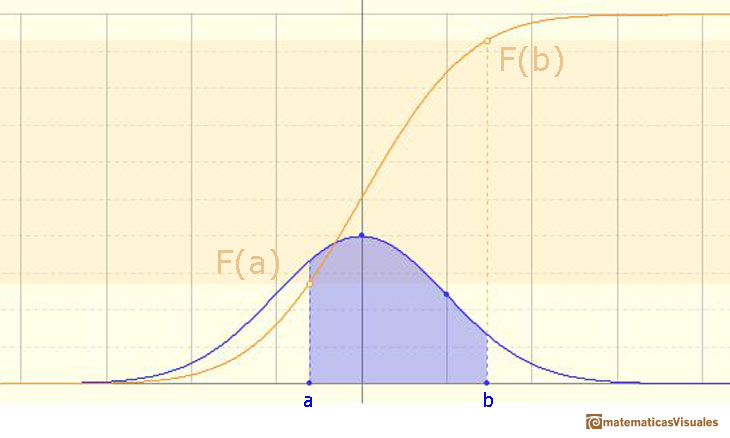
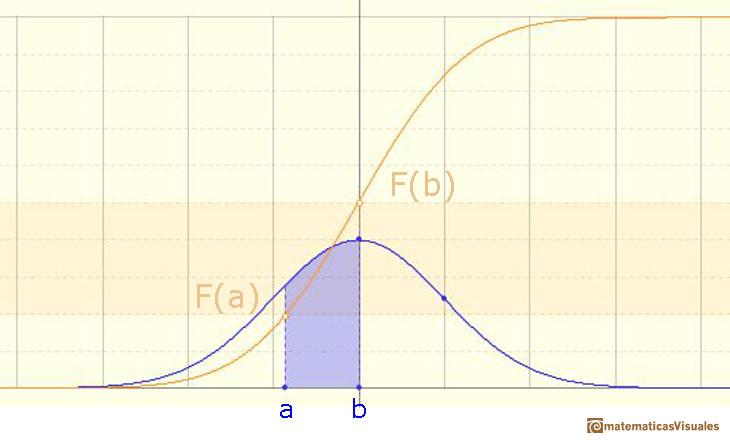
Podemos calcular muchas probabilidades, por ejemplo:
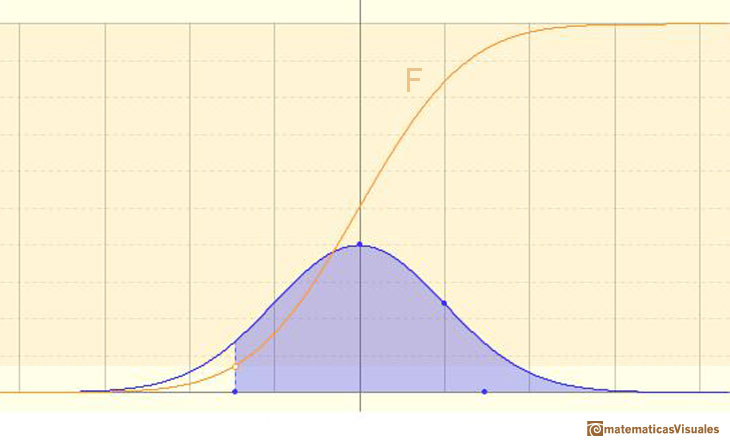
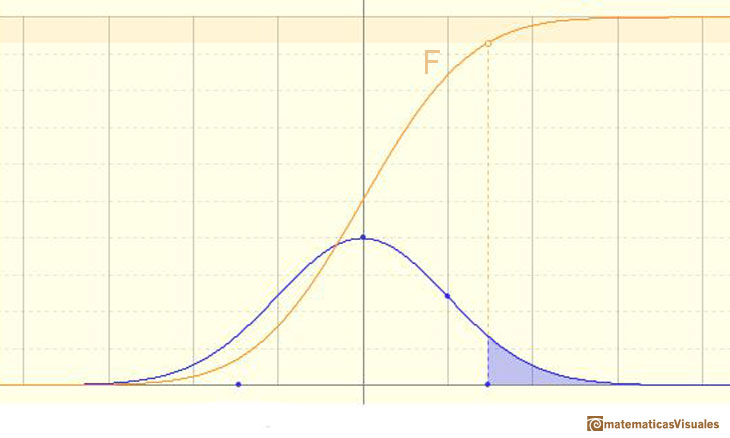
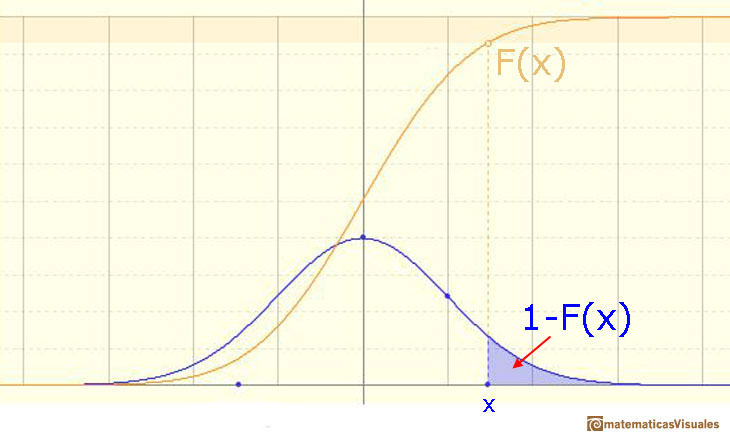
Podemos escribir:
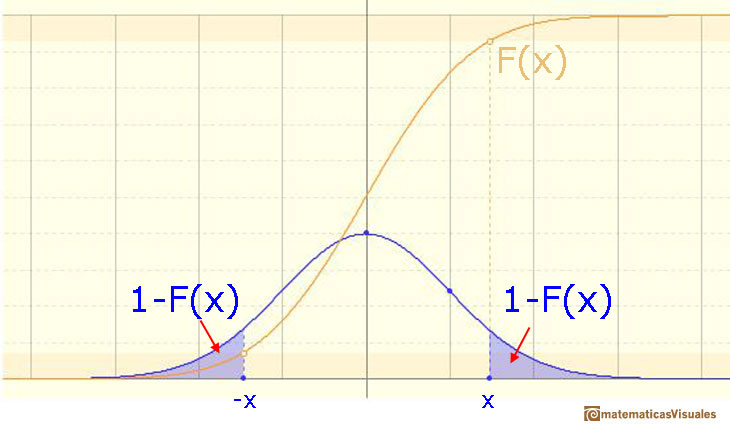
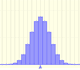
Podemos modificar los parámetros de la distribución normal.
La media está representada por un triángulo y se puede interpretar como un punto de equilibrio. Al arrastrarlo se modifica la media.
Arrastrando el punto sobre la curva (que es uno de los dos puntos de inflexión de la curva) se modifica la desviación típica.
El punto azul sobre el eje X representa el valor x de la variable. Al moverlo vemos el cambio de valor de la función de distribución.
Podemos ver la función de distribución (acumulada) y cómo cambia cuando modificamos la media (una simple traslacion) y la desviación típica (reflejando una mayor o menor dispersión de la variable).
Los puntos rojos controlan la escala vertical y horizontal de la gráfica.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES