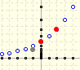Representación gráfica de progresiones geométricas. Suma de los términos de una sucesión geométrica. Series geométricas.

Algunas series geométricas se pueden sumar fácilmente. Podemos ver un ejemplo muy intuitivo cuando la razón es 1/4

La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.

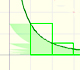A partir de una función positiva decreciente podemos definir series y aplicar el test de la integral. El test de la integral es un criterio que nos puede ayudar a decidir si una serie converge o diverge. Además, si la serie converge nos dará cotas.

La constante de Euler se define como una serie convergente.

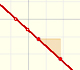Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.

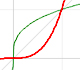Potencias con exponente natural son funciones importantes pues son la base de los polinomios. Sus funciones inversas son las raíces que son funciones potencia con exponente racional positivo.

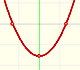Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.

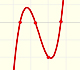Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.

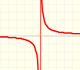Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.

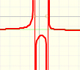Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).

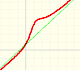Para valores grandes en valor absoluto de la variable x algunas funciones se comportan como una recta oblicua. A esta recta la llamamos asíntota oblicua de la función.

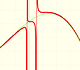Podemos añadir un polinomio a una función racional propia. El comportamiento asintótico de esta función racional será muy parecido al del polinomio.

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

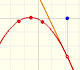La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

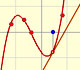La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

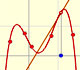Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.

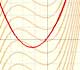Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.

La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.

Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.

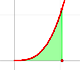La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.

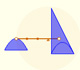Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.

Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.

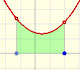Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.

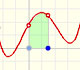Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).

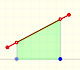Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.

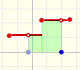Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.

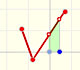Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.

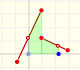En general, las funciones lineales a trozos no son continuas. Hay puntos en los que un pequeño cambio en la x produce un salto en el valor de la función.

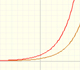Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.

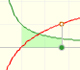Integrando la hipérbola equilátera podemos definir una nueva función que es el logaritmo natural.

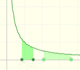Hemos definido la función logaritmo como una integral de la hipérbola equilátera. Esta integral tiene una importante propiedad que nos permitirá usar los logaritmos para transformar multiplicaciones en sumas.

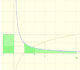Usando los logaritmos podemos multiplicar dos números haciendo una suma: el logaritmo de un producto es igual a la suma de los logaritmos de los factores.

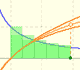El número e se puede definir como áquel cuyo logaritmo es 1. Partiendo de esta definición podemos aproximar su valor.

El número e, la base de los logaritmos naturales, se puede definir como una integral o como el límite de una sucesión relacionada con el interés compuesto. Ambas definiciones coinciden.

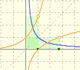Partiendo de la definición de logaritmo podemos definir la exponencial como su inversa.

Diferentes hipérbolas permiten definir logaritmos y exponenciales (sus inversas).

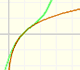Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

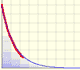Las funciones exponenciales pueden modelar la desintegración radioactiva.

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

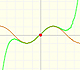Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.

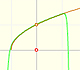La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

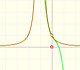La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

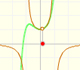La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.

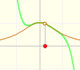La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.