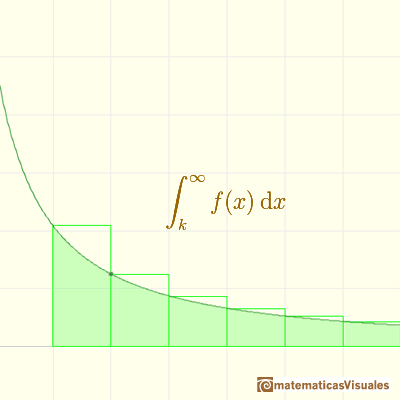
Si partimos de una función positiva y decreciente
Podemos definir
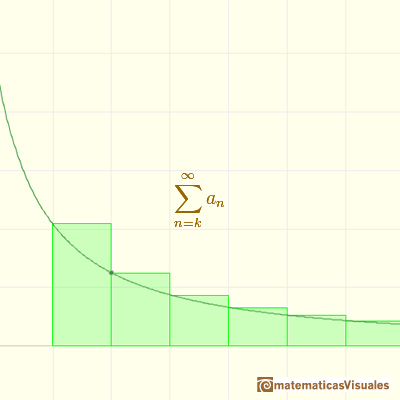
Y obtenemos una serie de términos positivos
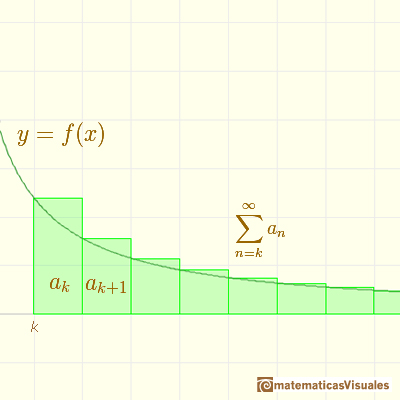
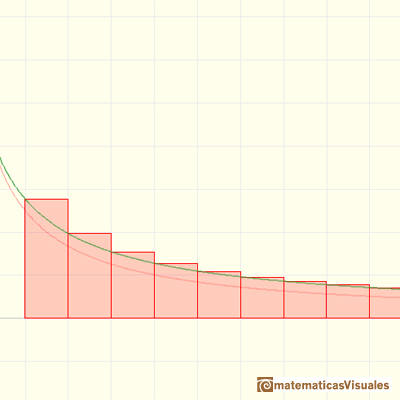
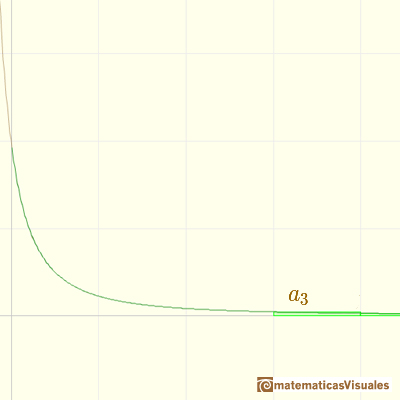
La suma de la serie es la suma de las áreas de un conjunto infinito de rectángulos (con base 1).
En la imagen vemos que esta suma es mayor (podría ser igual) que la integral.
En general, se verifica esta desigualdad:
En el mathlet podemos jugar con un caso particular
Arrastrando los puntos verdes podemos modificar lambda y p y obtenemos nuevas funciones de ese tipo.
En estos casos, las series que se obtienen son semejantes a p-series (trasladadas y expandidas o contraídas).
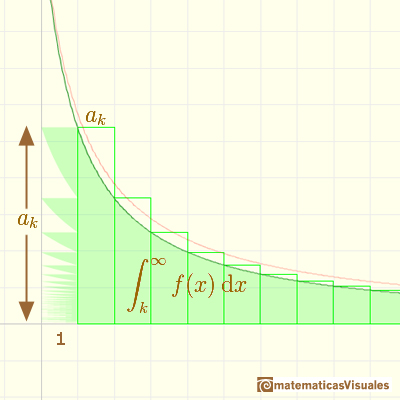
En el mathlet, pulsando el botón de la animación podemos ver que la serie es la integral más algo que es menor que
el primer término, ak.
Por ejemplo, consideremos la integral
Entonces
La serie converge y las cotas inferior y superior son:
MÁS ENLACES

Algunas series geométricas se pueden sumar fácilmente. Podemos ver un ejemplo muy intuitivo cuando la razón es 1/4

La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.

La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.
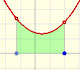
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
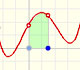
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
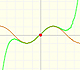
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
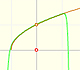
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
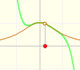
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.

La función exponencial compleja extiende la función exponencial real al plano complejo.
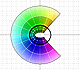
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

La función coseno compleja transforma rectas horizontales en elipses cofocales.
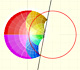
La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.

El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
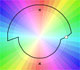
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.

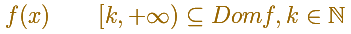
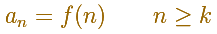
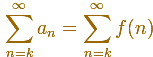
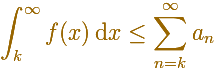
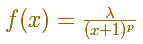
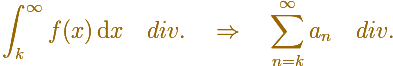
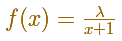
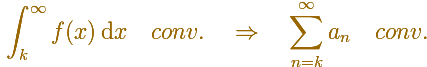
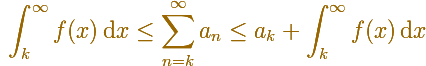
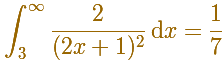
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR






































