Gamma, la constante de Euler, se define
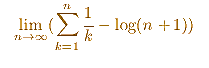
También se suele definir, equivalentemente, así:
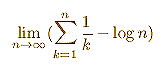
Usaremos la primera definición.
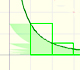
Se puede ver que esta serie está acotada por 1 y que es
creciente. Cada suma parcial se obtiene, a partir de la anterior, añadiendo un "triángulo"
bajo la hipérbola equilátera. Por el Teorema de Bolzano-Weiestrass, podemos afirmar que la serie
es convergente.
Mascheroni la nombró Gamma.
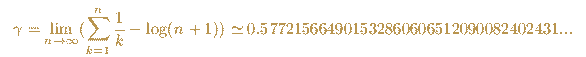
Gamma es una constante importante en Matemáticas. Se sospecha que es un número irracional
pero no se ha podido probar.
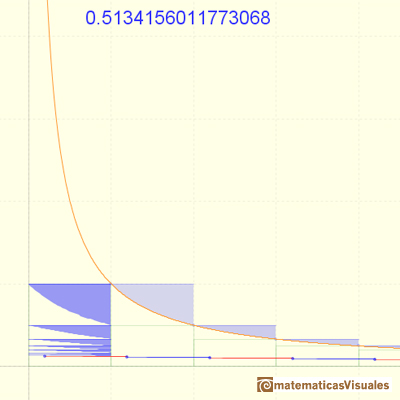
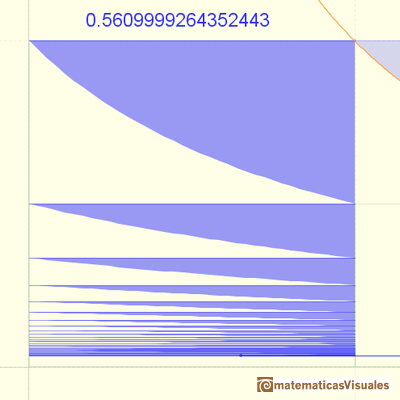
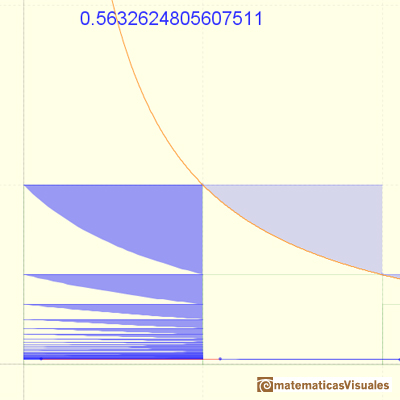
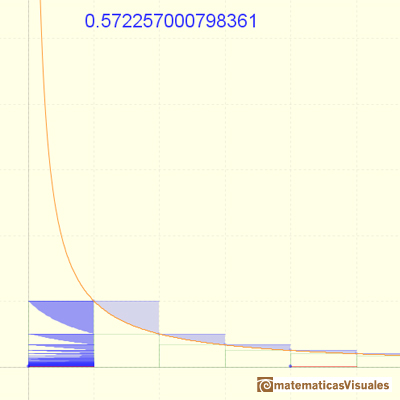
La convergencia de la serie es muy lenta.
El vídeo se ha grabado usando un applet desarrollado en Java.
Las sumas parciales están acotadas por 1. La serie es creciente. La serie es convergente y podemos ver que su valor será algo mayor que 0.5.
MÁS ENLACES
La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.
Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.
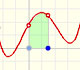
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.
El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.
El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
Un polinomio de grado n tiene n ceros o raíces.
La función exponencial compleja extiende la función exponencial real al plano complejo.
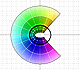
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.
La función coseno compleja transforma rectas horizontales en elipses cofocales.
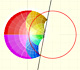
La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.
El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
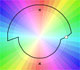
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.
Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.
ANTERIOR
