Ya sabemos que cos(z) es periódica con periodo 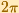 .
.
En esta página vamos a explorar cómo una recta horizaontal es tranformada por la función cos(z), siguiendo el libro de Tristan Needham Visual Complex Analysis.
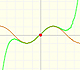
Con la animación podemos ver que la imagen de
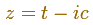
es "un óvalo simétrico" (que es el resultado de la suma de dos movimientos circulares).

Para calcular dónde este óvalo corta al eje real, consideramos
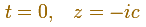
Entonces
El óvalo corta al eje real en este punto:
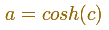
Para calcular dónde el óvalo corta al eje imaginario, consideramos
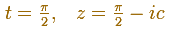
Entonces
El óvalo corta al eje imaginario en este punto:
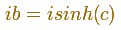
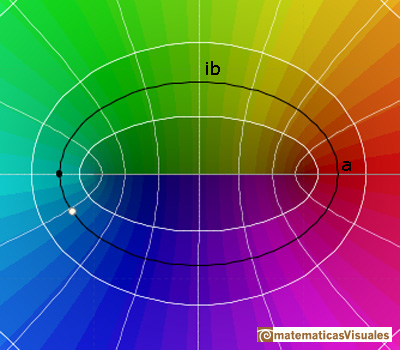
El ovalo es una elipse perfecta. Si calculamos
Usando
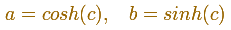
Considerando las partes real e imaginaria:
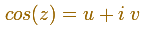
Podemos escribir
Que es la representación familiar de la elipse y que podemos escribir (fórmula impícita):
Para calcular los focos de la elipse podemos usar
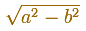

La forma de estas elipses varía al cambiar c pero todas ellas son elipses cofocales.
La imagen por cos(z) de una recta vertical es una hipérbola que tiene los mismos focos que las elipses. Elipses e hipérbolas se cortan en ángulos rectos.
REFERENCIAS
ENLACES