La función exponencial compleja es la función que podemos definir como la serie de potencias que
extiende la función exponencial real al plano complejo.
Esta serie converge en todo el plano complejo.
En esta página intentamos mostrar la naturaleza geométrica de esta función:
La función exponencial verifica:
La función exponencial es periódica con periodo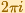 .
.
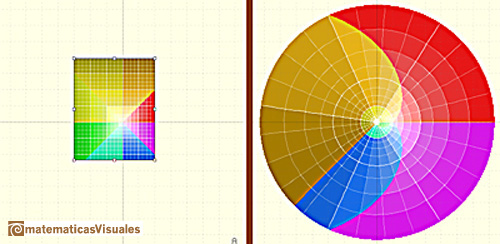
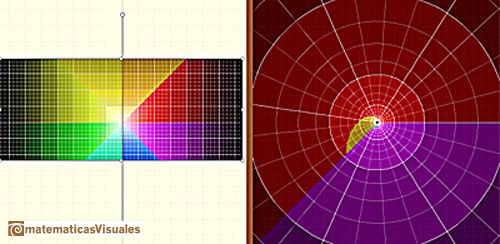
Cualquier banda horizontal del plano complejo de altura 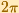 se transforma en todo el plano complejo (con la excepción del origen).
se transforma en todo el plano complejo (con la excepción del origen).
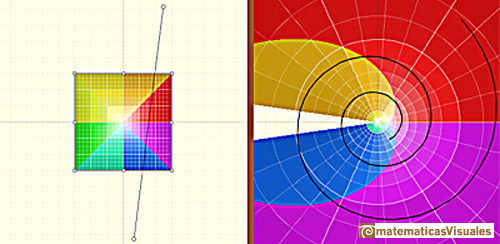
Una recta se transforma en una espiral (o en una recta o en una circunferencia).
La fórmula de Euler
puede interpretarse como que la función exponencial enrolla el eje imaginario alrededor de la circunferencia
unidad (Tristan Needham).
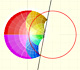
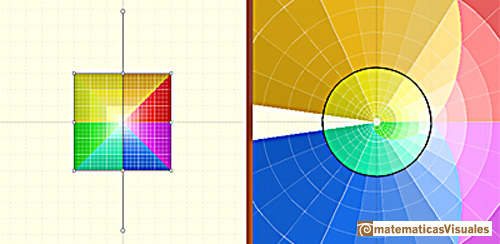
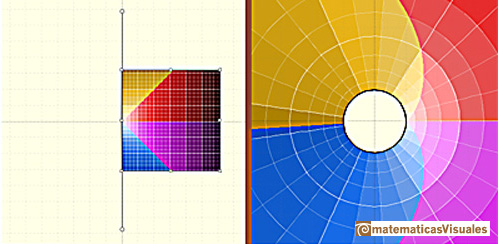
El semiplano a la izquierda del eje imaginario se mapea en el interior del círculo unidad, y el
semiplano a la derecha del eje imaginario se mapea al exterior del círculo unidad.
Las imágenes de cuadrados pequeños se asemejan a cuadrados y (en relación con esto) dos rectas que se intersectan
se mapean en curvas que se intersectan con el mismo ángulo (Tristan Needham).
MÁS ENLACES

Las potencias de exponente natural tienen un cero de multiplicidad n.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.

Podemos controlar qué partes del plano complejo se muestran con colores.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

La función coseno compleja transforma rectas horizontales en elipses cofocales.
La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.

La inversión preserva la magnitud de los ángulos pero invierte el sentido. Circunferencias ortogonales se transforman en circunferencias ortogonales

El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.
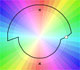
Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.
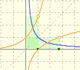
Partiendo de la definición de logaritmo podemos definir la exponencial como su inversa.
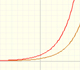
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

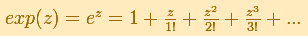
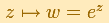
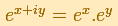
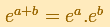
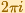 .
.
 se transforma en todo el plano complejo (con la excepción del origen).
se transforma en todo el plano complejo (con la excepción del origen).
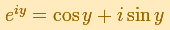
 SIGUIENTE
SIGUIENTE






















 ANTERIOR
ANTERIOR








