La definición usual de función es restrictiva. Podemos ampliar la definición de una función si permitimos que f(z) tenga varios valores diferentes para un valor de z. En este caso, decimos que f es una "función multivaluada" o una multifunción.
Por ejemplo, sabemos que
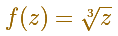
tiene tres valores diferentes (si z es distinto de 0), por lo tanto, es una multifunción.
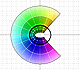
En este caso, vemos que cada color se muestra tres veces y que cada valor z tiene tres imagenes diferentes con el mismo módulo pero con distinto argumento.

Si elegimos arbitrariamente una de estas tres imágenes de un punto z dado y nos movemos gradualmente desde esta posición inicial, entonces la imagen también se mueve de una manera completamente determinada: su distancia al origen es la raíz cúbica de la distancia de z y la velocidad angular es un tercio de la de z. (Needham, p.91)
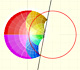
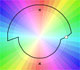
Si z se mueve a lo largo de un bucle como el de la figura, su imagen f(z) se mueve a lo largo de un bucle cerrado y vuelve a su valor original.
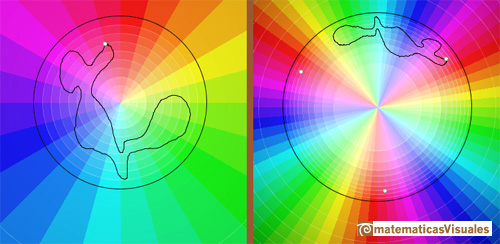
Sin embargo, si z se mueve a lo largo de un bucle que rodea al origen una vez, entonces f(z) no vuelve a su valor original sino que termina en una raíz cúbica diferente. Notamos que la forma particular del bucle es irrelevante, lo que importa es que rodea al origen una vez. (Needham, p.91)

Análogamente, si z se mueve a lo largo de un bucle que rodea al origen dos veces, entonces f(z) termina en la tercera y última raíz cúbica. (Needham, p.91)
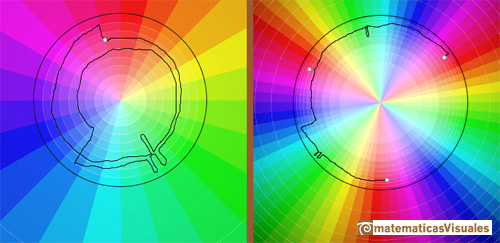
Claramente, si z se mueve a lo largo de un bucle que rodea al origen tres veces, entonces f(z) vuelve a la primera raíz. (Needham, p.91)
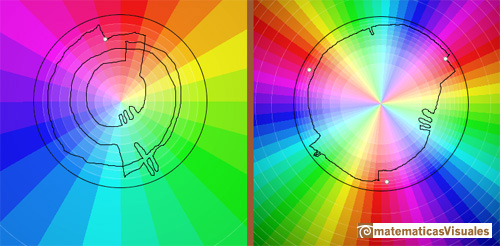
El punto z 0 = se llama punto de ramificación de la multifunción f(z).
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES