Ya hemos visto que las funciones cuadráticas reales pueden tener, como mucho, dos raíces o ceros reales.

Al considerar una función cuadrática en el plano complejo siempre tiene dos raíces. Es un caso particular del polinomio de grado n que, por el Teorema fundamental del Álgebra, tiene n raíces.

En el vídeo empezamos representando la función

Las dos raíces (o ceros) de esta función son los números reales 1 y -1. Se les llama raíces de la unidad.

Si movemos los puntos estamos cambiando las raíces del polinomio y podemos ver representaciones de una función de grado 2 más general (con dos raíces que pueden ser complejas):

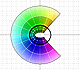
Al transformar cada punto del plano obtenemos un nuevo punto al que se le asocia un color. De algún modo, estos colores se corresponden con las coordenadas en polares.

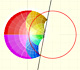
En la representación, una familia de curvas puede verse como las curvas de nivel de la superficie modular de la función. Los puntos que están en la misma curva se caracterizan porque el producto de las distancias a los ceros es una constante. Es decir, estas curvas son los óvalos de Cassini y, entre ellos, la lemniscata.

Estos óvalos fueron estudiados por Cassini y propuestos como posible trayectoria de los planetas antes de que Newton zanjara el asunto. Ya eran conocidos por el matemático griego Perseo (hacia el año 150 a.C.) como secciones de un toro.

Se han refinado los colores próximos a cero para que al acercarnos con la lupa a uno de ellos podamos intuir que el comportamiento de un cero de un polinomio es "como si fuera un cono" y las curvas de nivel son muy próximas a circunferencias.

Podemos mover (despacio) los puntos que representan las dos raíces o ceros. En este función podemos ver que esas raíces son los focos de los óvalos de Cassini.

Si las dos raíces coinciden entonces decimos que la raíz es doble.

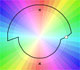
En el caso de la raíz doble podemos ver que la sucesión de colores (rojo, amarillo, verde, azul) se repite dos veces alrededor de la raíz.

En la siguiente variante del applet podemos usar una cuadrícula de colores (o cambiar a un código de colores basado en círculos concéntricos). Se pueden mostrar (banda en negro), los puntos que se tranforman en complejos con módulo "próximos" a 1.

Este es un ejemplo cuando el código de colores es una cuadrícula:

El mismo polinomio cuando lo representamos con un código en polares:

Puede verse una explicación del siguiente vídeo en este enlace:

MÁS ENLACES

Funciones polinómicas complejas (4): Polinomio de grado n

Un polinomio de grado n tiene n ceros o raíces.

Funciones polinómicas complejas (5): Polinomio de grado n (variante)

Podemos controlar qué partes del plano complejo se muestran con colores.

Funciones polinómicas (1): funciones afines

Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.

Funciones polinómicas (2): funciones cuadráticas

Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.

Funciones polinómicas (3): funciones cúbicas

Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.

Funciones polinómicas (4): Polinomios de interpolación de Lagrange

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.

Cero y polo

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Cero y polo (variante)

Tenemos más control sobre qué partes del plano complejo se representa con colores.

Transformaciones de Moebius

Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.

Función exponencial compleja

La función exponencial compleja extiende la función exponencial real al plano complejo.

La función coseno compleja

La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

La función coseno compleja: transformación de una recta horizontal

La función coseno compleja transforma rectas horizontales en elipses cofocales.

Inversión

La inversión es una transformación del plano que transforma rectas y circunferencias en rectas y circunferencias.

Inversion: una transformación anticonforme

La inversión preserva la magnitud de los ángulos pero invierte el sentido. Circunferencias ortogonales se transforman en circunferencias ortogonales

Multifunciones: Potencias con exponente fraccionario

El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.

Multifunciones: Dos puntos de ramificación

Una multifunción puede tener más de un punto de ramificación. La multifunción considerada en esta página tiene dos valores y dos puntos de ramificación.

Polinomios de Taylor: función exponencial compleja

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

Polinomios de Taylor: función coseno compleja

La función coseno compleja tiene un desarrollo de Taylor que converge en todo el plano complejo.

Polinomios de Taylor: función racional compleja con 2 singularidades

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.