





A raíz de una pregunta de mis alumnos de Bachillerato estamos estudiando la familia de funciones polinómicas de grado 2 que dependen del parámetro p.
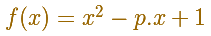
Ya hemos visto esta familia de funciones desde el punto de vista de la variable real.
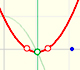
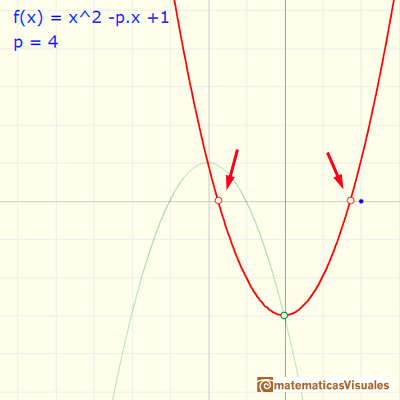
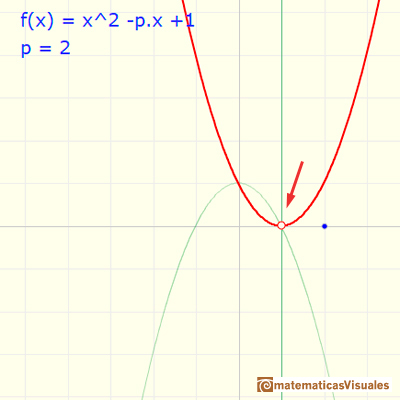
Sabemos que para unos valores del parámetro p la función tiene dos ceros reales distintos, en dos casos tenemos una raíz real doble y en otros casos la función tiene dos ceros complejos.
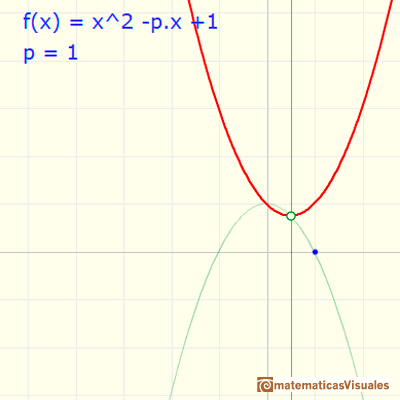
Vamos a estudiar ahora estos ceros desde el punto de vista de la variable compleja.
No es raro usar la letra z para indicar que la variable es compleja:
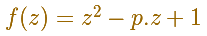
Usaré una repesentación de las funciones complejas con una técnica que aprendí de Frank Farris - Visualizing complex-valued functions in the plane.
Esta página quiere tener el espíritu del libro 'Visual Complex Analysis' del profesor Tristan Needham.
Para mi fue un honor que el profesor Needham citara mi sitio matemáticasVisuales como sitio relacionado con su libro 'Visual Complex Analysis'
En la siguiente animación vamos a ver cómo al variar el parámetro p varían las raíces.
Esas raíces se representan con color blanco. Al principio de la animación vemos las dos raíces reales distintas, las raíces se confunden en una raíz doble (p=2) y pasan a ser complejas. Vuelven a unirse como raíz doble real (p=-2) y se separan en dos raíces reales distintas negativas.
Si p=3 las dos raíces son reales, positivas, inversas:

Si p se acerca a 2 las raíces reales se van aproximando:
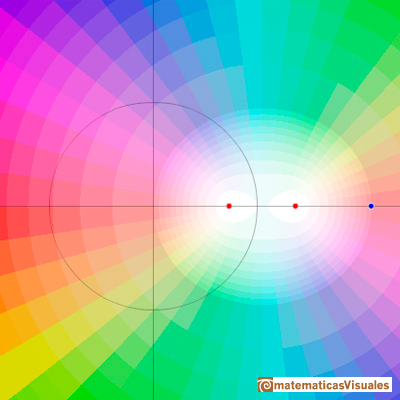
Las dos raíces reales están muy próximas:
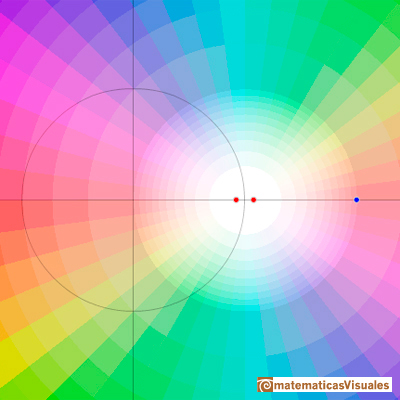
Si p=2 las dos raíces reales se confunden y decimos que es una raíz real doble:
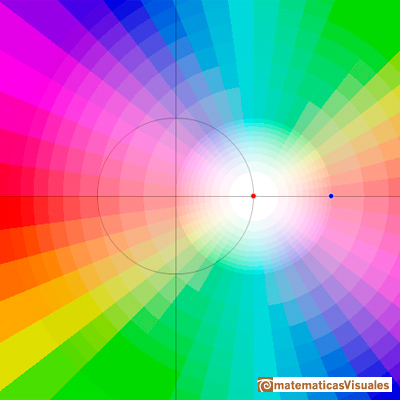
Para valores de p entre 2 y -2 las raíces son complejas conjugadas y de módulo 1. Recorren la circunferencia unidad:
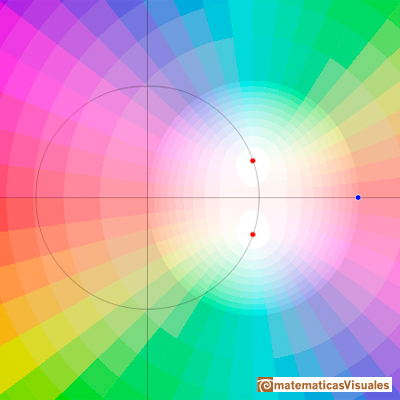
En este caso p=1
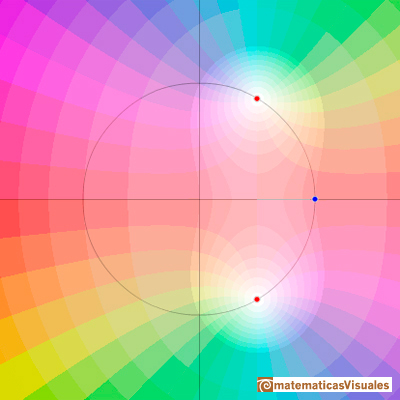
Las raíces complejas de la función si p=0 son especialmente sencillas. La curva que las rodea y que pasa por el origen es una curva llamada lemniscata:
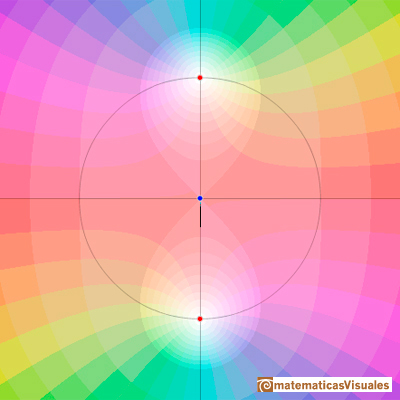
Para valores negativos de p, como p=-1 se produce una situación simétrica a la de su opuesto:
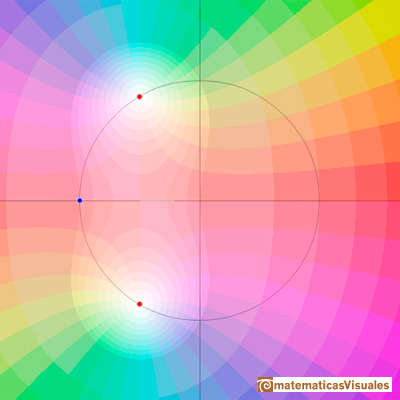
Las raíces vuelven a ser reales si p=-2 (raíz real doble negativa) y para valores menores son reales distintas y negativas.
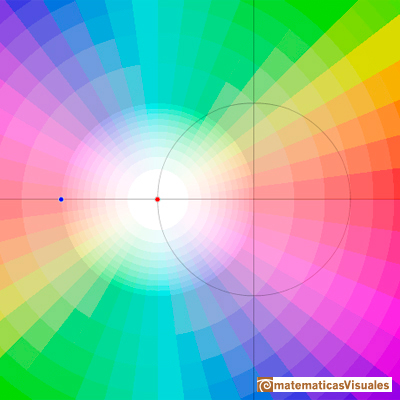
Vamos a fijarnos en la representación de las raíces. En estos casos la raíz es simple. En torno a ella, los colores dan 1 vuelta:

p=simple

p=0 simple

Pero si nos fijamos en el comportamiento cuando la raíz es doble vemos que los colores dan dos vueltas en torno a la raíz. Si hubiera una raíz triple (de un polinomio de grado mayor o igual que 3) los colores darían tres vueltas.

Variante del vídeo en la que se hace zoom sobre una de las raíces.
 ANTERIOR
ANTERIOR
MÁS ENLACES












