En casa: Funciones cuadráticas que dependen de P
Esta página surge como primera respuesta a una cuestión que me han planteado mis alumnos de Bachillerato.
Se trata de estudiar y clasificar esta familia de funciones polinómicas de grado 2 que dependen del parámetro p.
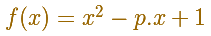
Ya hemos tenido ocasión de estudiar las funciones polinómicas de grado 2.
Las funciones cuadráticas son polinomios de grado 2. Sus gráficas son parábolas. Para encontrar los puntos de corte con el eje de abcisas tenemos que resolver una ecuación. El vértice de la parábola es un máximo o mínimo de la función.
Antes de resolver el problema, vamos a aprovechar para repasar algún concepto en estos casos particulares.
Fíjate cómo cambia la función según va cambiando el valor del parámetro p.
Nos fijamos en que la parábola cambia de posición pero no de forma.
Todas las parábolas tienen un eje de simetría. Cambiando el valor del parámetro p se va desplazando el eje de simetría.
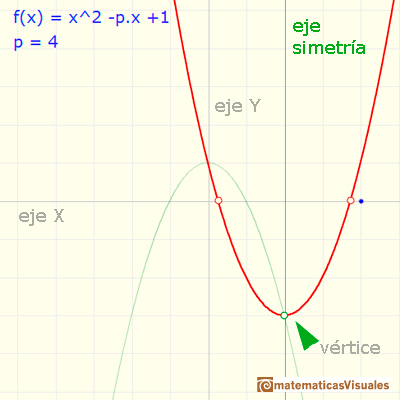
La ecuación del eje de simetría es:
En todas las parábolas de esta familia el vértice es un mínimo. La coordenada x del vértice:
La coordenada y del vértice es:
Completando cuadrados se puede obtener una fórmula de nuestras parábolas en la que se destaca las coordenadas del vértice:
Fíjate que el vértice cambia de posición siguiendo una parábola. ¿Sabes justificar el motivo? ¿Y calcular la ecuación de esta parábola que recorre el vértice al cambiar el parámetro p?
Ahora vamos a pasar a plantear el problema de clasificar esta familia de funciones cuadráticas que dependen del parámetro p según el número de 'ceros' de la función (o raíces reales del polinomio)
Hacer esta clasificación significa hacer una partición del conjunto de los números reales.
En este caso vamos a hacer tres partes pues sabemos que un polinomio de grado 2 tiene siempre dos raíces (por el Teorema Fundamental del Álgebra).
Esas dos soluciones pueden ser:
- Dos raíces reales distintas.
- Una raíz real (que es doble).
- Dos raíces complejas.
La clave está en el discriminante:
Vamos a ver esos casos en la familia de funciones que estamos estudiando.
Si p=4 la función tiene dos ceros reales distintos positivos. Fíjate que sean reales o complejas las dos raíces son inversas. ¿Sabes justificar por qué?
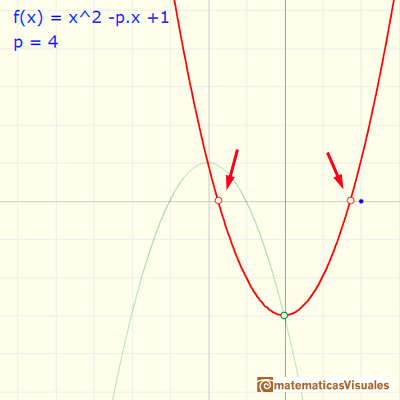
Cuando p=2.1 las dos raíces están próximas, casi se confunden.
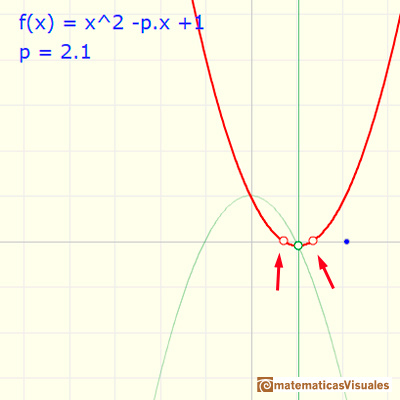
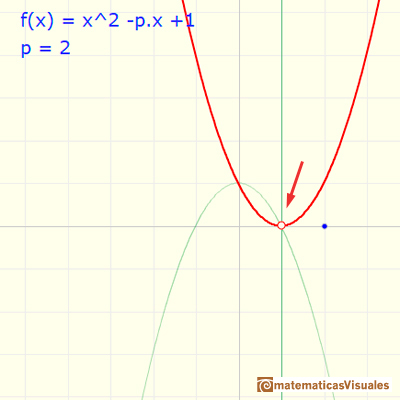
Si p=2 las dos raíces se han confundido. Decimos que la raíz es doble. Coincide con el vértice. La fórmula es ahora una 'identidad notable'.
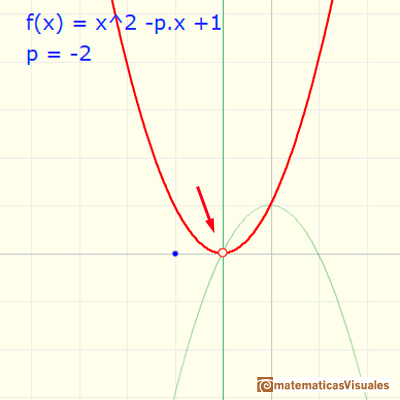
La situación se repite si p=-2. Ahora la raíz doble es negativa.
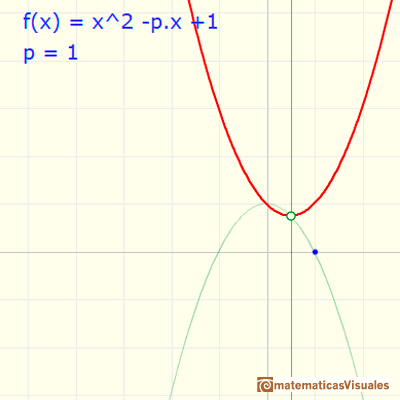
En el caso p=1 nos encontramos con que la parábola no corta al eje x. La función no tiene ceros reales, por lo tanto, tiene dos ceros o raíces complejas.
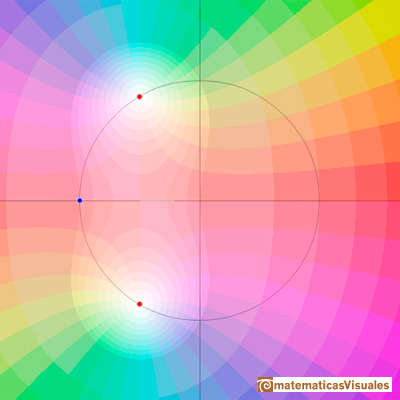
Las dos raíces complejas son conjugadas, inversas y de módulo 1. ¿Sabes justificarlo? ¿Sabes calcularlas?
¿Las raíces complejas de un polinomio de grado 2 con coeficientes reales son siempre conjugadas?
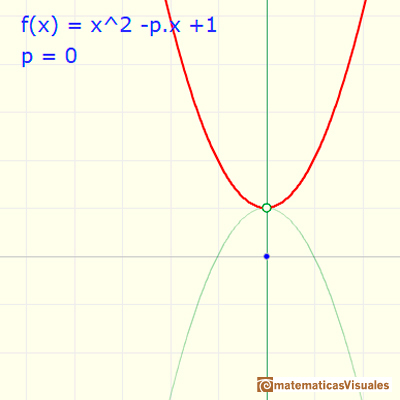
Si p=0 las dos raíces complejas son especialmente sencillas.
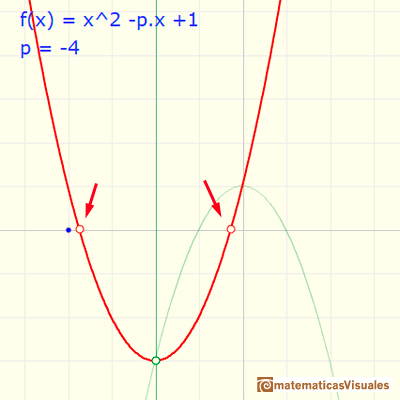
Con valores negativos de p la situación es simétrica a los valores positivos. En la siguiente ilustración se muestra el caso p=-4 con dos raíces reales distintas y negativas.
Las particiones de los números reales que hacemos en este tipo de ejercicios suelen ser:
- Vacías. El conjunto vacío.
- Un intervalo o unión de intervalos. Es decir, son subconjuntos con infinitos elementos. 'Montones grandes'.
- Un conjunto discreto, es decir, uno o varios números reales. Un subconjunto finito de números reales. 'Montones pequeños'. Estos conjuntos discretos se corresponden con situaciones que podemos considerar excepcionales.
Por ejemplo, en este caso 'lo raro' sería que tenga una raíz doble pues tiene que coincidir que la parábola toque (sea tangente) al eje x.
¿Te animas a resolver este problema? La propuesta es redactar una respuesta completa estudiando esta familia de funciones cuadráticas y hacer una clasificación. Enviar un documento o fotografía a mi contacto para su publicación.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
Respuesta de Ana María, desde Alcalá de Henares
En el siguiente enlace vamos a estudiar qué ocurre con las raíces de esta familia de polinomios en el plano complejo:
Estamos en casa: Una familia de funciones polinómicas que depende de un parámetro. Raíces complejas.
Estudio de las raíces reales o complejas de una familia polinómica de grado 2 que depende de un parámetro. Representación gráfica en el plano complejo.
ANTERIOR
MÁS ENLACES
Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.