Como ya hemos visto al estudiar la serie geométrica de razón 1/4, la serie
geomética
es fácil de sumar cuando la razón es menor que 1. Decimos que la serie es convergente y su suma es:
Un caso sencillo es cuando la razón es
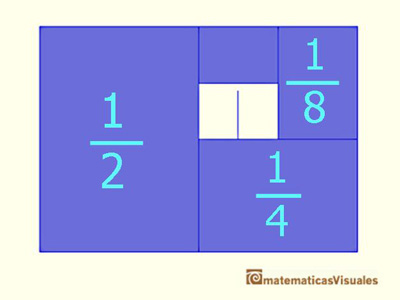
Entonces, la serie que queremos sumar se puede representar así:
Y la suma de la serie geométrica cuya razón es un medio es:
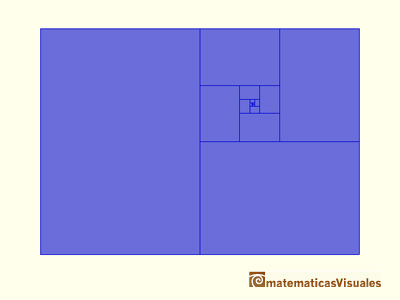
En este visualización hemos usado una proporción del rectángulo inicial de modo que al partirlo por la mitad
siempre haya resultado que los nuevos rectángulos tienen la misma proporción. Se trata de la proporción que usamos
en muchas ocasiones para el papel, por ejemplo, la hoja DIN A4.
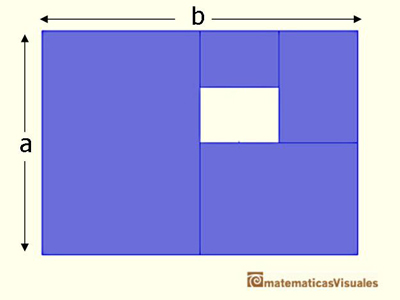
La proporción entre el largo y el ancho del rectángulo es:
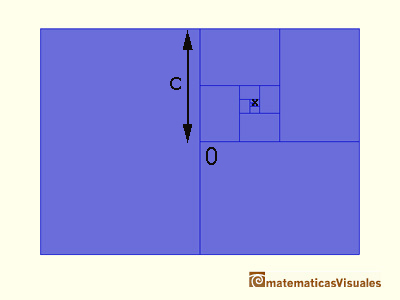
Los rectángulos se van marcando formando una especie de espiral alrededor de un punto. ¿Puedes deducir cuales son las
coordenadas de ese punto? Está relacionado con otra serie geométrica: la serie geométrica de razón 1/4.
MÁS ENLACES
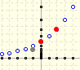
Representación gráfica de progresiones geométricas. Suma de los términos de una sucesión geométrica. Series geométricas.
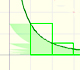
A partir de una función positiva decreciente podemos definir series y aplicar el test de la integral. El test de la integral es un criterio que nos puede ayudar a decidir si una serie converge o diverge. Además, si la serie converge nos dará cotas.
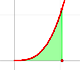
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
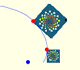
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.

En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
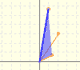
Se puede ver como una rotación dilatativa.
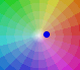
Geométricamente, la multiplicación por un complejo es una transformación del plano que consiste en una rotación y una expansión o contracción (rotación dilatativa).

Una progresión geométrica compleja está relacionada con las espirales equiangulares.

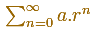
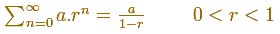
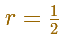
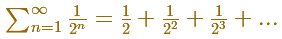
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR