Rotaciones dilatativas (o semejanzas en espiral) son casos particulares de transformaciones que llamamos semejanzas.
Las semejanzas son transformaciones que cambian cada figura en en figuras que tienen la misma forma, preservando los ángulos, "aunque pueden cambiarse las distancias. Sin embargo, todas las distancias se aumentan (o disminuyen) en la misma proporción que llamamos razón de semejanza" (Coxeter and Greitzer, p.94)
En los applets y en las imágenes he usado una ilustración clásica de 'Las aventuras de Alicia en el País de las Maravillas' dibujadas por John Tenniel.
Si una semejanza preserva distancias entonces es una isometría. Las isometrías transforman cada figura en una figura congruente. Por lo tanto, las semejanzas incluyen, como casos particulares, a las isometrías.
Las isometrías más sencillas son las traslaciones.
Una rotación es una semejanza que es también isometría:
"El tipo más sencillo de semejanza es una dilatación que transforma cada línea en una línea paralela. Una dilatación que no es una traslación se llama dilatación central, porque todas las rectas que unen puntos correspondientes de una figura y su imagen son concurrentes." (Coxeter and Greitzer, p.94). Las dilataciones centrales también se llaman homotecias.
Los semigiros (simetría central o media vuelta) son isometrías que pueden verse como rotaciones o como dilataciones centrales.
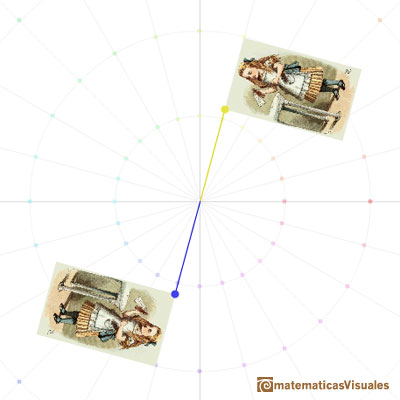
Las dilataciones centrales tienen un punto invariante y es cierto que cualquier dilatación que no sea una traslación tienen un único punto invariante (ver Coxeter, p. 69).
La combinación de una dilatación central y una rotación respecto del mismo centro se llama una rotación dilatativa o semejanza en espiral.
En el siguiente vídeo podemos ver una rotación dilatativa como una transformnación continua: primero, rotación y después, dilatación.
Las rotaciones dilatativas se llaman también semejanzas en espiral pues podemos verlas como transformaciones continuas que siguen el camino de una espiral equiangular.
REFERENCIAS
SIGUIENTE
ANTERIOR
MÁS ENLACES
