Espiral equiangular. Rotación
Coxeter escribió sobre la espiral equiangular (o espiral logarítmica):
"Descartes fue el primero que reconoció esta curva. Jacob Bernouilli (1654 - 1705) la encontró tan
fascinante que dió instrucciones para que la grabaran en la lápida de su tumba, con la inscripción
Eadem mutata resurgo
Estas palabras ("Aunque cambiada, surgiré igual") expresan uns consecuencia notable de la manera en la
que la curva se puede desplazar sobre sí misma mediante una rotación dilatativa:
cualquier dilatación tiene sobre ella el mismo efecto que una rotación, y viceversa.
" (Coxeter)
Coxeter hace referencia a Steinhaus quién describe esta propiedad como una ilusión óptica: "Si giramos el libro alrededor del
vértice, la espiral parece crecer más grande o más pequeña. Dos espirales que tienen el mismo ángulo con el radio constante
son congruentes." (Steinhaus). Steinhaus relaciona la espirales logarítmicas con caminos de persecución.
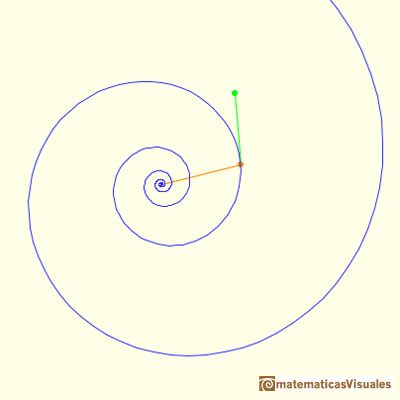
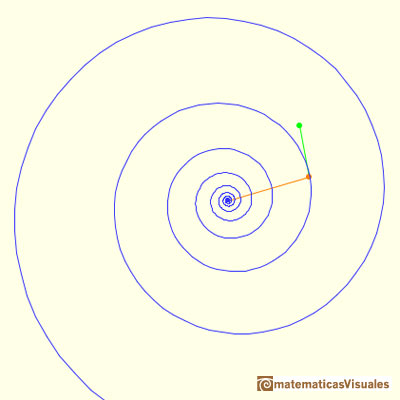
Moviendo los puntos cambiamos el vector posición y la dirección de la tangente.
Otro ejemplo de espiral equiangular.
REFERENCIAS
Coxeter - Fundamentos de Geometría. Ed. Limusa. (pag. 155)
Steinhaus - Instantáneas matemáticas. Ed. Salvat (pag. 132).
D'Arcy Thompson - On Growth and Form. (Cambridge University Press)
MÁS ENLACES
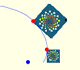
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.
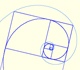
Dos espirales equiangulares contienen los vértices de rectángulos áureos.

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
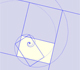
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
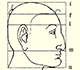
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
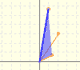
Se puede ver como una rotación dilatativa.




















 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR





