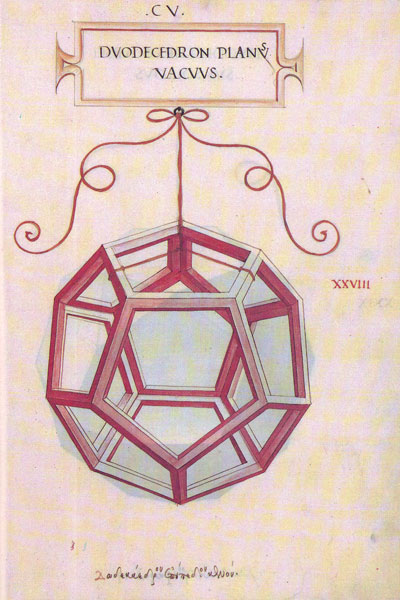
Leonardo da Vinci dibujó dos dodecaedros
para el libro de Luca Pacioli 'La Divina Proporción'.
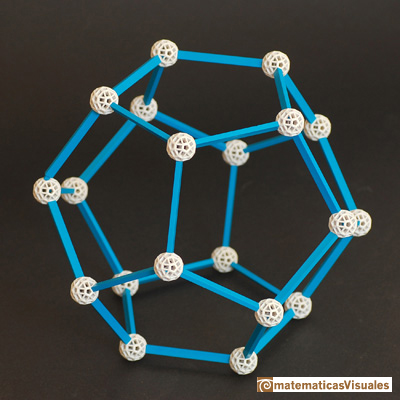
Kepler también estuvo interesado en este cuerpo geométrico. Por ejemplo, podemos ver este dibujo en su libro 'Harmonices Mundi - La harmonía del mundo (1619)'.
(Podemos leer el libro original en Posner Memorial Collection):
En el libro de Durero 'Underweysung der Messung' el autor publicó el primer desarrollo plano de un dodecaedro regular (y de varios poliedros más).
Un dodecaedro regular es un poliedro platónico que tiene 12 caras que son pentágonos regulares.
Hay una profunda relación entre el dodecaedro y la proporción áurea.
Los puntos de coordenadas:
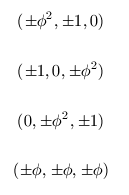
Son los 20 vértices de un dodecaedro regular de arista 2.
Donde 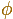 es la razón áurea que hemos
podido ver en el rectángulo áureo.
es la razón áurea que hemos
podido ver en el rectángulo áureo.
Podemos calcular la distancia entre pares de vértices adyacentes para convencernos por nosotros mismos.
Podemos construir este poliedro usando Zome:
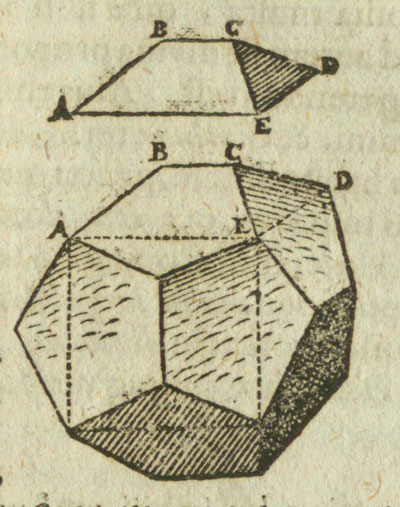
Kepler nos mostró cómo se puede poner un cubo dentro de un dodecaedro regular:
Podemos inscribir un cubo en un dodecaedro de modo que cada lado del cubo está en una cara del dodecaedro uniendo dos vértices alternos
de la cara, como una diagonal del pentágono.
(Ball and Coxeter, p. 131)
Un dodecaedro regular se puede inscribir en una esfera. Para calcular el radio de esa esfera podemos pensar que es el centro de uno de los cubos que
se pueden poner dentro del dodecaedro. Estos cubos tienen arista que es phi (el número áureo) si el dodecaedro tiene arista 1.
También podemos razónar con estas figuras hechas con Zome. Entonces
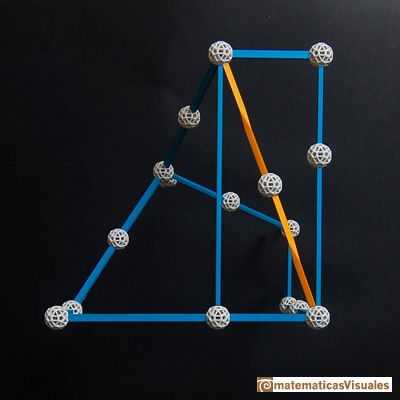
Para calcular el volumen de un dodecaedro podemos tener en cuenta que el volumen de un dodecaedro de lado 1 es un octavo del volumen del
dodecaedro de arista 2. Puede ser interesante fijarse en esta figura:
Con la ayuda de Zome Zome estudiaremos
el volumen de un dodecaedro regular.
Origami: construcción de un dodecaedro con módulo
PHiZZ de Tom Hull.
Origami: construcción de un dodecaedro con el módulo penultimate (puede aprender
sobre el módulo penultimate):
El dodecaedro y el icosaedro son poliedros duales.
Podemos construir un dodecaedro y un icosaedro con los lados correspondientes perpendiculares, bisecándose uno a otro. Entonces, la
parte común es un icosidodecaedro. (Ball and Coxeter, 136)
Si quieres ver cómo construir poliedros y descargar plantillas puedes ir a
Construcciones de poliedros. Técnicas sencillas. Cartulina: cara a cara.
El Icosidedocaedro tiene 20 caras triangulares y 12 pentagonales. Es un juguete para una mascota matemática:
Los vértices del dodecaedro (20) y los vértices del icosaedro (12) son los vértices de un triacontaedro rómbico:
El triacontaedro y el icosidodecaedro son poliedros duales, del mismo modo que lo son el dodecaedro y el icosaedro.
Una construcción muy bonita e interesante es el compuesto de 5 tetraedros en un dodecaedro.
Puedes ver varias técnicas distintas de construcción de esta figura en el siguiente enlace:

Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
REFERENCIAS
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999 (p. 121)
MÁS ENLACES

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

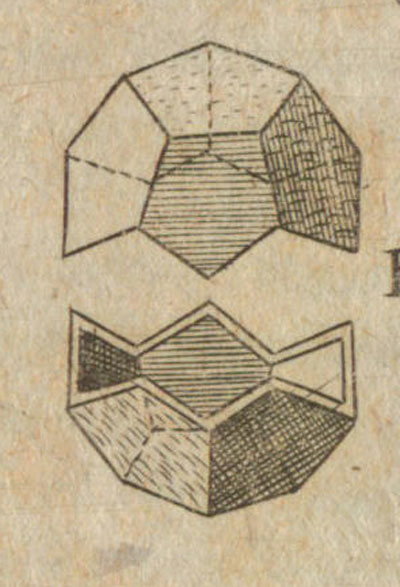
Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
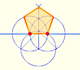
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
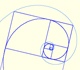
Dos espirales equiangulares contienen los vértices de rectángulos áureos.
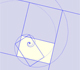
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

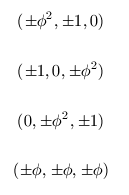
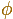 es la razón áurea que hemos
podido ver en el rectángulo áureo.
es la razón áurea que hemos
podido ver en el rectángulo áureo.













 ANTERIOR
ANTERIOR



































 SIGUIENTE
SIGUIENTE





