Dibujo de un pentágono con regla y compás
Partiendo de un segmento podemos dibujar un pentágono regular usando solamente regla y compás de modo que este segmento sea un lado del pentágono.
Ya sabemos que la diagonal de un pentágono regular y su lado están en proporción áurea
y que la razón áurea se denota por
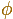y que su valor es:
Este es el paso fundamental:
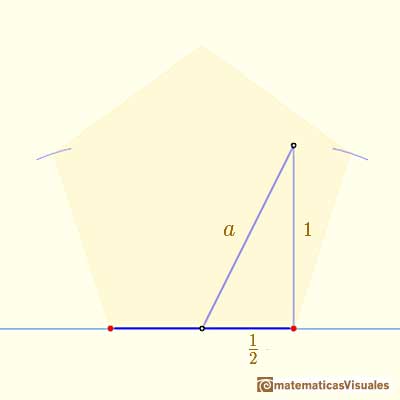
Entonces el valor de a es:
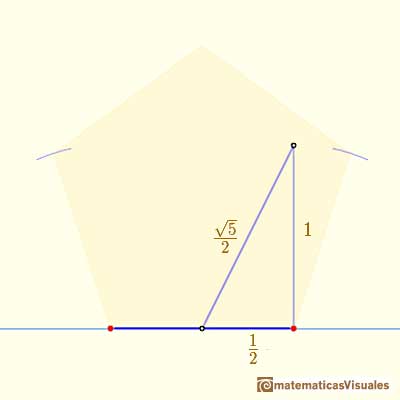
Podemos dibujar un segmento que tenga la longitud de la diagonal de un pentágono regular:
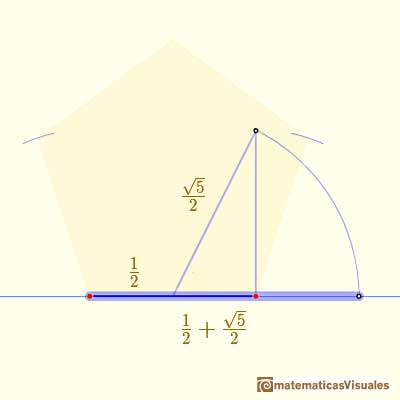
Fácilmente terminamos nuestro trabajo y obtenemos un pentágono regular:
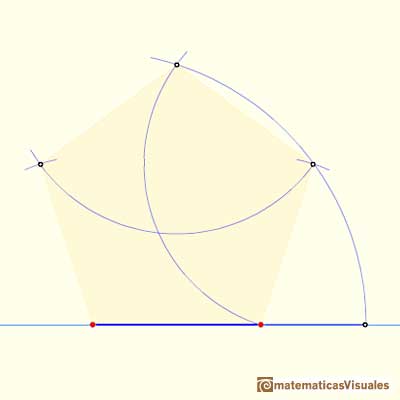
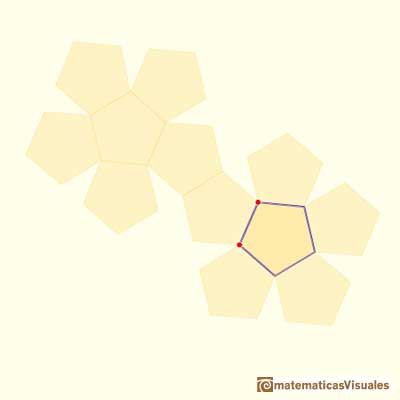
Dibujando doce pentágonos obtenemos el desarrollo plano de un dodecaedro:
SIGUIENTE
A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.
ANTERIOR
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.
MÁS ENLACES
Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.
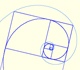
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.
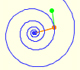
La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
Dos espirales equiangulares contienen los vértices de rectángulos áureos.
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
Con tres rectángulos áureos podemos construir un icosaedro.
Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
Cualquier dilatación de una espiral equiangular tiene el mismo efecto que una rotación.
En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.