El teorema de Pitágoras es uno de los teoremas más famosos de las Matemáticas. Se trata de una propiedad de los triángulos rectángulos.
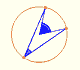
Un triángulo es rectángulo si uno de sus ángulos es un ángulo recto (el ángulo C en la imagen).
Los dos lados que forman el ángulo recto se llaman catetos y el lado opuesto se llama hipotenusa (el lado c de la imagen).
En la ilustración, el cateto a es el lado opuesto al ángulo A y el cateto b es el cateto opuesto al ángulo B. Esta notación de lados y ángulos es muy típica.
Si movemos el punto C nos daremos cuenta de que está siempre sobre un arco de circunferencia. Es la circunferencia circunscrita al triángulo. El diámetro de esa circunferencia es la hipotenusa. Esto es una propiedad muy interesante, un caso particular de la propiedad de los ángulos incrito y central. Puedes explorar una demostración de este hecho en el siguiente enlace:
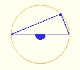
El teorema de Pitágoras afirma que el cuadrado de la hipotenusa es igual a la suma (de las áreas) de los cuadrados de los catetos.
Desde un punto de vista geométrico, el teorema nos habla de áreas y nos dice que el cuadrado grande tiene la misma área que el área de los otros dos cuadrados juntos.
En esta página podemos interactuar con una demostración dinámica e interactiva de este teorema de Pitágoras inspirada en la que hizo Euclides en su libro "Los Elementos".
En su demostración, Euclides usó triángulos en vez de paralelogramos pero la demostración es esencialmente la misma. Podemos ver una representación de la demostración de Euclides en las siguientes fotos tomadas en la puerta de la Universidad de Berlín.


En la demostración usamos la idea de que si un paralelogramo es transformado por un cizallamiento (preservando la base y la altura), el área del paralelogramos permanece constante. En nuestro caso, los cuadrados de los catetos se transforman en rombos.
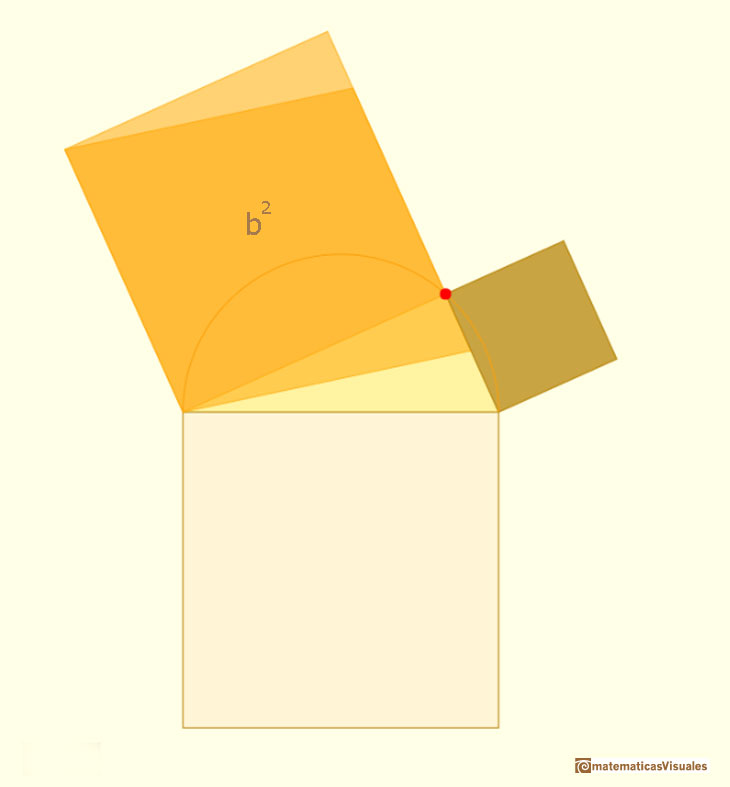
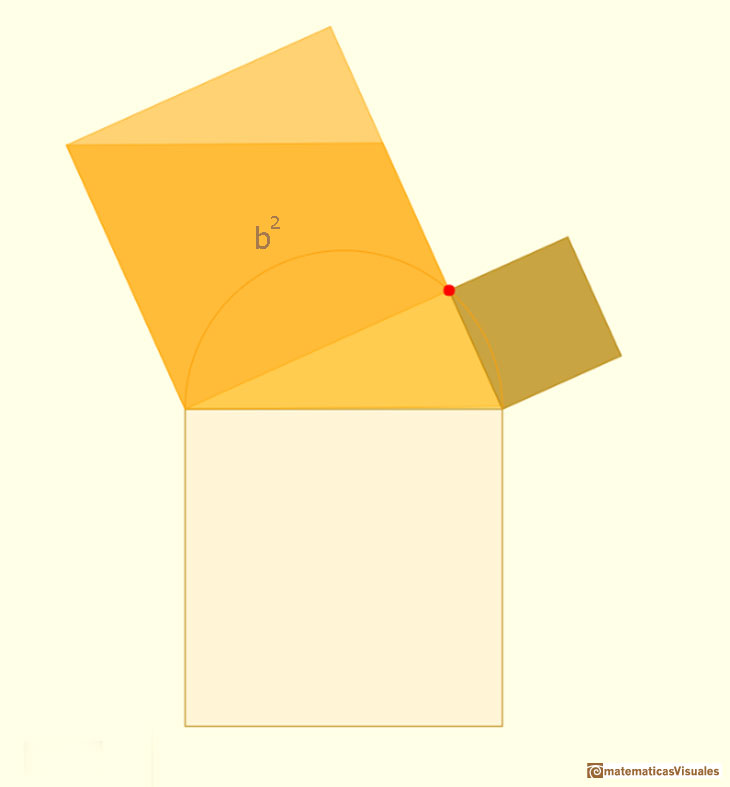
Si después consideramos un movimiento (de rotación, en nuestro caso) el área tampoco cambia.
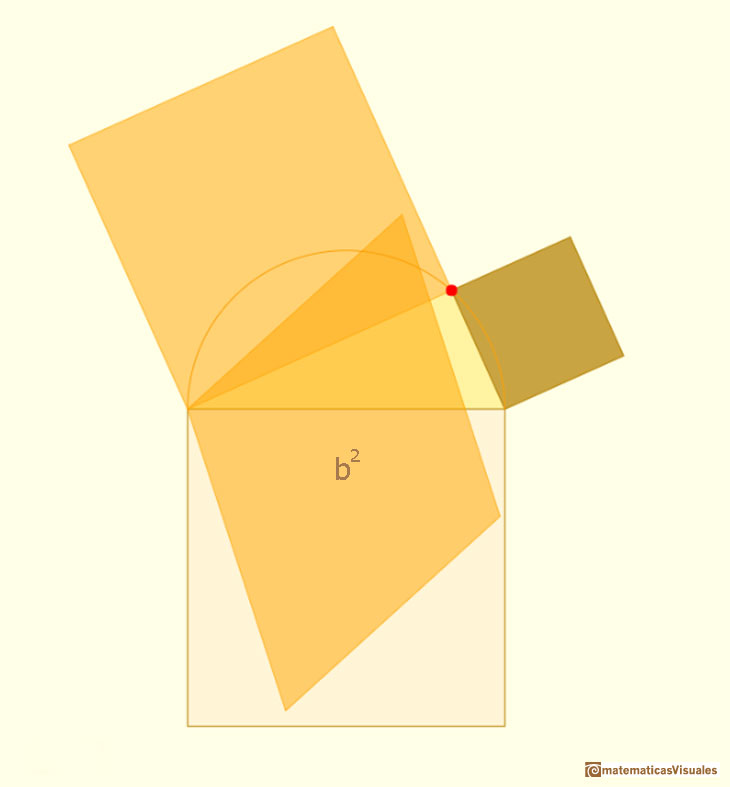
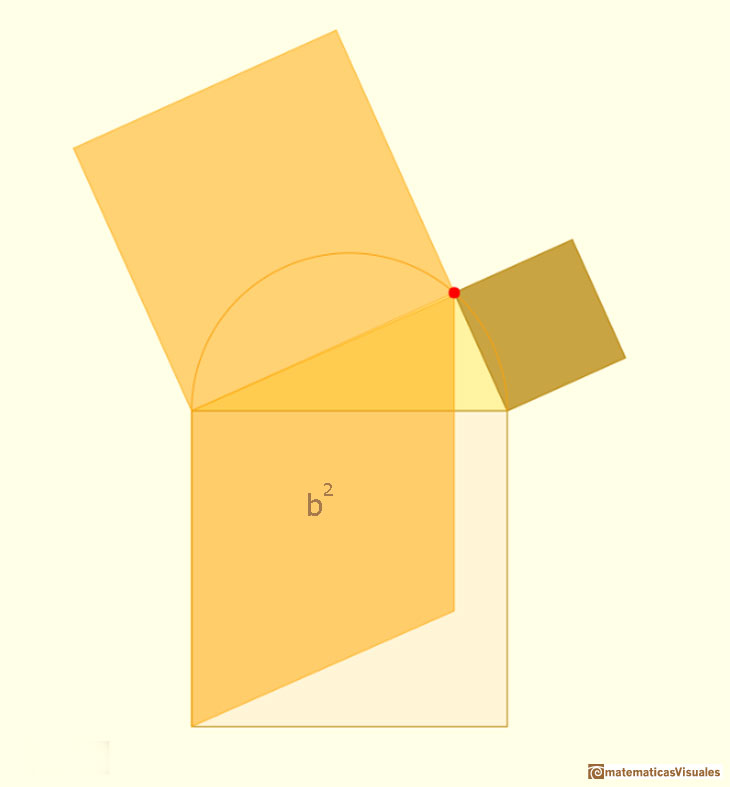
Después consideramos otro cizallamiento, en este caso en vertical. El rombo es ahora un rectángulo que ocupa una parte del cuadrado sobre la hipotenusa:
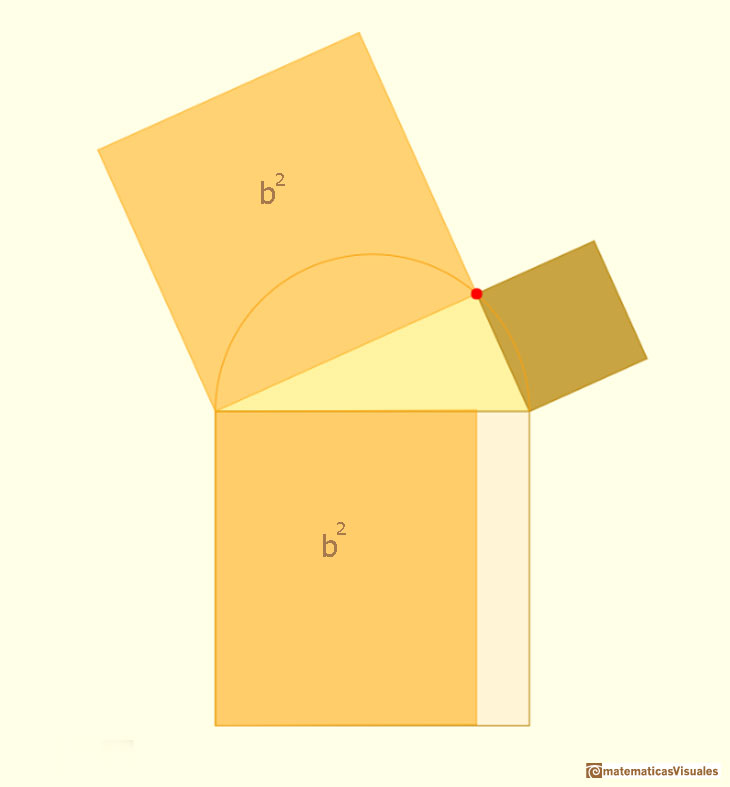
Hacemos lo mismo con el otro cateto a.
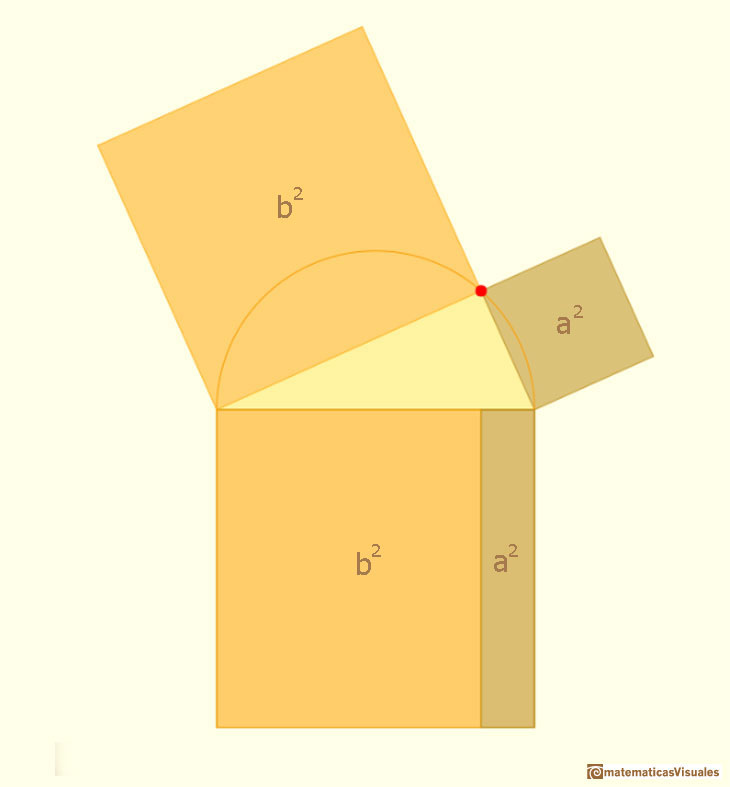
Los dos cuadrados de los catetos transformados cubren el cuadrado de la hipotenusa. Queda probado el teorema de Pitágoras:
Esta demostración tiene la ventaja de que nos muestra otra propiedad de los triángulos rectángulos.
En un triángulo rectángulo, si dibujamos la altura desde el angulo recto a la hipotenusa, esta queda dividida en dos segmentos.
Estos dos segmentos son las proyecciones de los dos catetos sobre la hipotenusa. Usaremos la notación a' y b'.
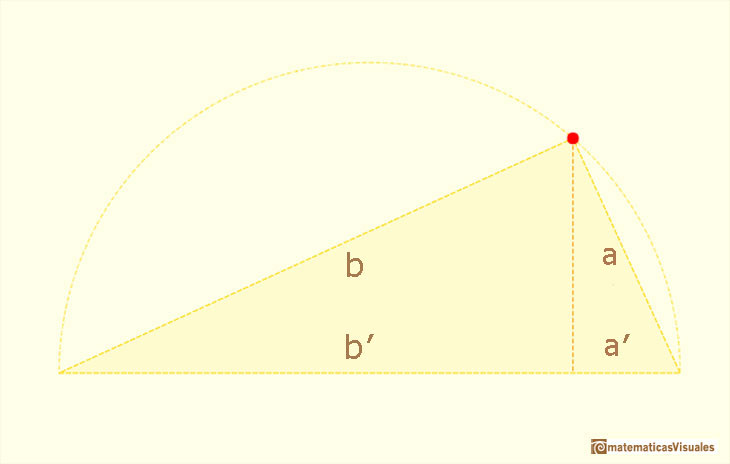
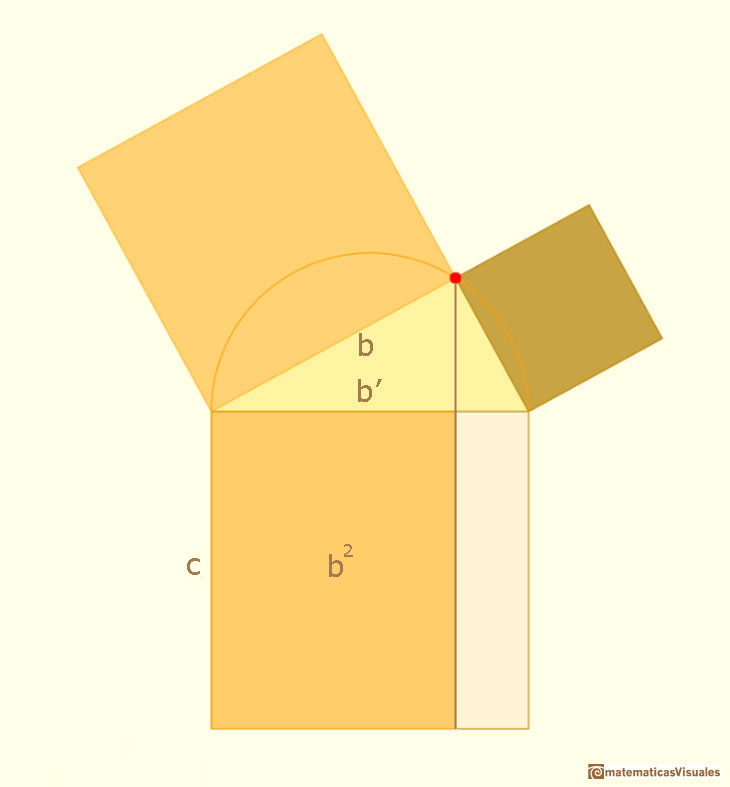
Si nos fijamos en el área de cada cuadrado sobre un cateto y la parte que cubre sobre el cuadrado de la hipotenusa podemos escribir:
Realmente no necesitamos el teorema de Pitágoras para probra este resultado (que, a veces, se conoce como teorema del cateto). Se puede deducir usando solamente semejanza.
Al trazar la altura sobre la hipotenusa se forman dos triángulos rectángulos que son semejantes entre sí y también semejantes al triángulo original.
¿Podrías probar este resultado usando semejanza?
A veces se usa el concepto de media geométrica y entonces este teorema se puede escribir:
La longitud de cada cateto de un triángulo rectángulo es la media proporcional de la longitud de la hipotenusa y la de la proyección de ese cateto sobre la hipotenusa.
Si quieres revisar algo más sobre semejanza y la media geométrica puedes seguir este enlace:
Uno de los triángulos rectángulos más simples tiene lados 3, 4 y 5. Es decir, está formado por tres números enteros.
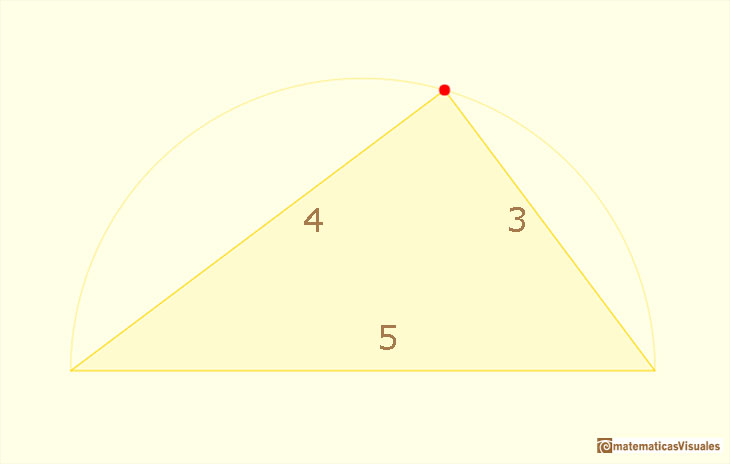
Los grupos de tres números enteros que verifican el teorema de Pitágoras, como 3, 4 y 5, se llaman ternas pitagóricas.
Vamos a terminar este comentario con una cita de John Stillwell que me parece muy interesante:
"Se piensa que en la Antigüedad estas soluciones pueden haberse usado para construir triángulos rectos. Por ejemplo, haciendo en un cuerda 12 nudos a la misma distancia y cerrándola obtenemos un triángulo (3, 4, 5) con un ángulo recto entre los lados 3, 4.
Sea o no este un método práctico para construir ángulos rectos, la existencia de una interpretación geométrica de un hecho puramente aritmético como
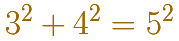
es una maravilla. A primera vista, aritmética y geometría paracen pertenecer a campos sin relación ninguna. La aritmética se basa en contar, la esencia de un proceso discreto (o digital). El hecho es que la aritmética puede entenderse claramente como la salida de un cierto proceso de contar y no esperamos que tenga ningún otro sentido más allá de este. La geometría, por otro lado, está relacionada con objetos continuos y no con objetos discretos, por ejemplo, líneas, curvas y superficies. Los objetos continuos no se pueden construir a partir de elementos simples a partir de procesos discretos y esperamos ver hechos geométricos más que llegar a ellos a través de cálculos.
El teorema de Pitágoras fue la primera pista de una oculta y profunda relación entre aritmética y geometría y ha continuado manteniendo una posición clave entre estos dos campos a través de la historia de las matemáticas. Unas veces ha sido una relación de cooperación y otras de conflicto, como lo que ocurrió después del descubrimiento de que la raíz de 2 es un número irracional. Esto es lo habitual cuando nuevas ideas emergen a partir de áreas de tensión, resolviendo un conflicto y permitiendo que ideas que previamente eran irreconciliables interactúen provechosamente. La tensión entre aritmética y geometría es, sin duda, la mas profunda en matemáticas y ha llevado a los teoremas más profundos. El teorema de Pitágoras es el primero de estos y el más influyente." (John Stillwell)
REFERENCIAS
MÁS ENLACES






















 SIGUIENTE
SIGUIENTE