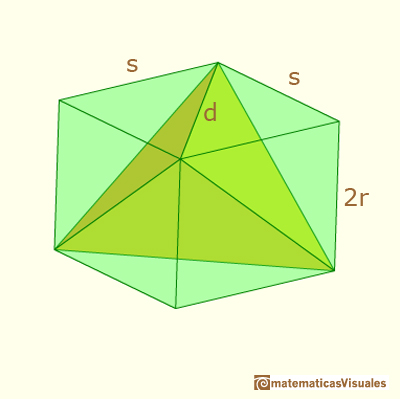
Howard Eves describe un tetraedro del siguiente modo:
... dibuja dos segmentos perpendiculares, cada uno de longitud
con el segmento que une sus puntos medios como perpendicular común."
La distancia entre estas dos líneas es 2r.
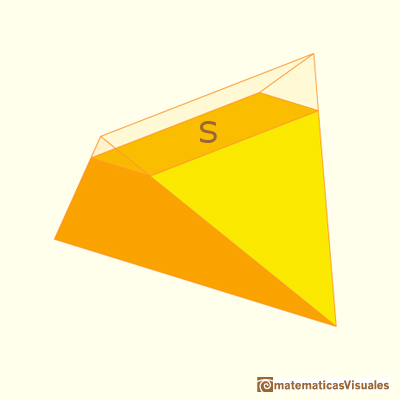
Este tetraedro se puede considerar dentro de un prisma de base cuadrada y altura 2r.
El lado del cuadrado es
Por lo tanto, el
volumen del tetraedro es
Si x es la distancia del plano de la sección que se representa en el applet al centro del tetraedro, el área
de la seccion es (es un caso particular de secciones en un tetraedro):
Ahora que sabemos cómo calcular el volumen de un tetraedro y las áreas de las secciones de un
tetraedro y de una esfera podemos
ver cómo Howard Eves mezcló estas ideas para calcular el volumen de una esfera usando el Principio de Cavalieri.
MÁS ENLACES

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

Estudiamos un tipo de poliedros inscritos en una esfera, en particular la llamada esfera de Campanus que fue muy popular durante el Renacimiento y que Luca Pacioli llamó Septuaginta.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.

Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.


 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR


























