Ya hemos visto que el volumen de un tetraedro (en general, no regular)
que podemos obtener uniendo algunas diagonales de las caras de un paralelepípedo es un tercio el volumen de ese
paralelepípedo.
En esta página vamos a ver las secciones de un tetraedro que podemos construir a partir de un paralelepípedo de base cuadrada.
En la posición inicial, el applet muestra un tetraedro regular cortado por la mitad en una sección cuadrada.
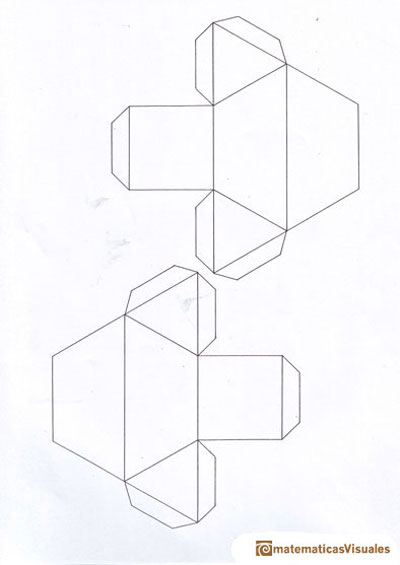
Es un rompecabezas conocido que está formado por dos piezas iguales con las que hay que construir un tetraedro.
Es fácil contruir estas dos piezas y hacer el rompecabezas con cartulina
(cada pieza está formada por dos tetraedros y medio octaedro):
Consideraremos unas secciones del tetraedro que son, en general, rectangulares. En el centro, la sección es un cuadrado.
Queremos calcular el área de estas secciones.
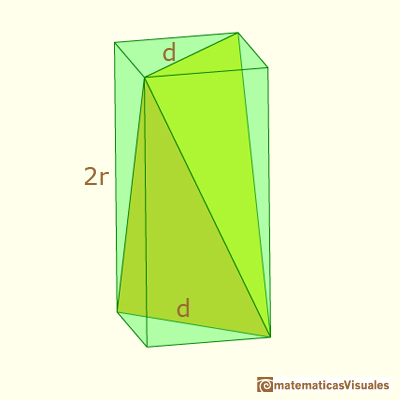
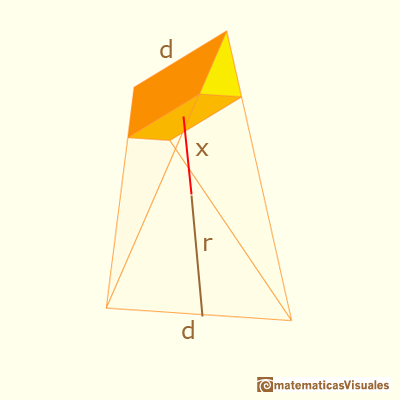
Partimos de un tetraedro dentro de un prisma recto de base cuadrada:
Si x es la distancia entre el centro y la sección:
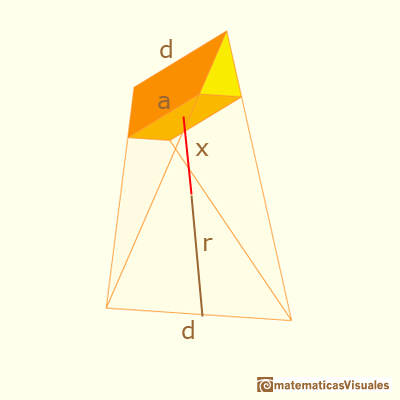
Podemos calcular el lado a:
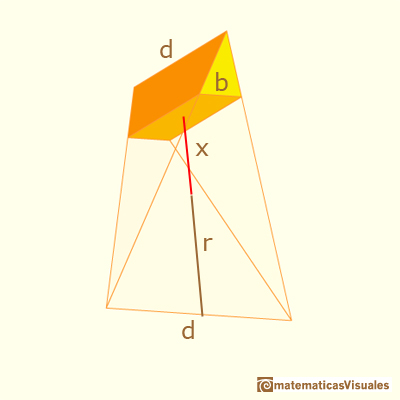
Y el lado b de la sección:
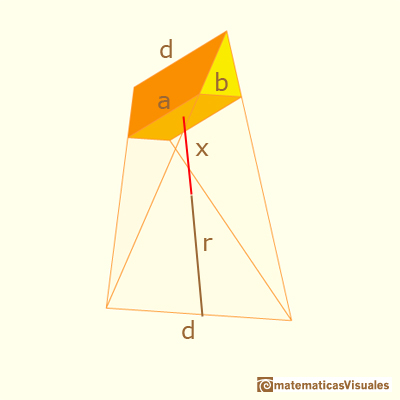
Entonces el área de la sección es:
Podemos hacer los mismos cálculos en un caso particular interesante en la página que dediamos a las
secciones en el tetraedro de Howard Eves.
MÁS ENLACES

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.

El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

Estudiamos un tipo de poliedros inscritos en una esfera, en particular la llamada esfera de Campanus que fue muy popular durante el Renacimiento y que Luca Pacioli llamó Septuaginta.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.






 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR