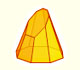
Una pirámide es un poliedro que tiene una cara poligonal que llamamos base y con las otras caras triangulares que tienen un punto en común (el vértice de la pirámide). Estas caras triangulares son las caras laterales.
Un caso particular es cuando la base puede inscribirse en una circunferencia. En el primer mathlet podemos podemos ver pirámides cuya base es un polígono regular. Si el vértice está en la perpendicular sobre el centro de la circunferencia decimos que la pirámide es recta. Llamaremos pirámide regular a una pirámide recta cuya base es un polígono regular.
El primer interés de esta página es mostrar cómo una pirámide se puede desarrollar en el plano.


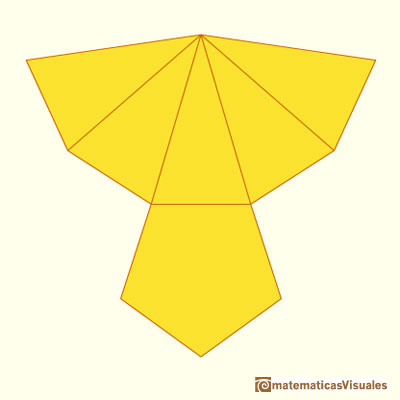
Este es el desarrollo plano de una pirámide pentagonal:
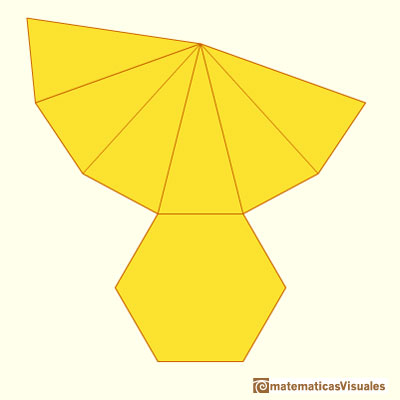
Otro ejemplo, el desarrollo plano de una pirámide hexagonal:
Para calcular la superficie lateral de una pirámide necesitamos la apotema de las caras. Esta apotema es la distancia desde el vértice de la pirámide al centro de un lado de la base, es decir, es la altura de una cara lateral. Por el Teorema de Pitágoras, hay una relación entre esta apotema y la altura de la pirámide.
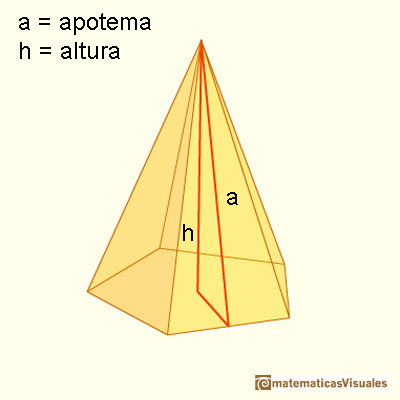
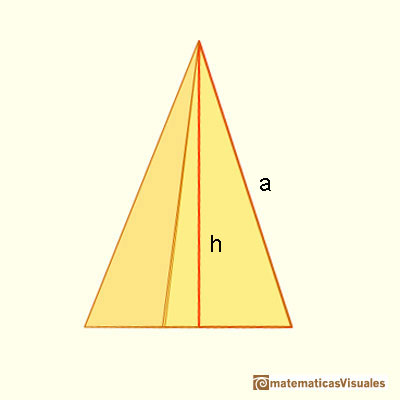
Vamos a calcular la superficie lateral de una pirámide. Si P es el perímetro de la base, la fórmula para la superficie lateral de una pirámide (las caras laterales son triángulos) es semejante a la fórmula para el área de un triángulo:
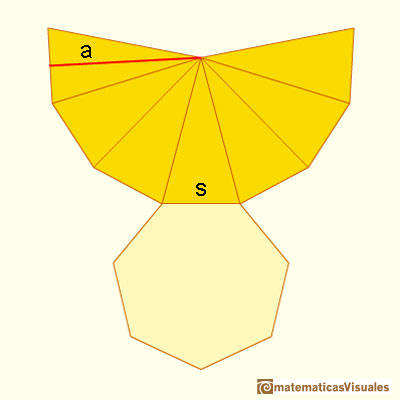
Cuando estudiemos la superficie lateral de un cono, la fórmula será similar (con un argumento análogo al que podemos ver en Kepler y el área del círculo.)
La pirámide más regular es un tetraedro. Es un sólido platónico que tiene cuatro caras que son triángulos equiláteros. Por lo tanto, un tetraedro es un caso particular de pirámide triángular.

Este es el desarrollo plano de un tetraedro:

Vamos a ver ahora las pirámides truncadas por un plano paralelo a la base.
Por ejemplo, una pirámide hexagonal truncada:

Y su desarrollo plano:
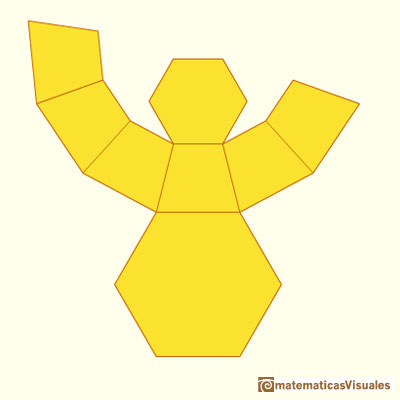
Otro ejemplo:
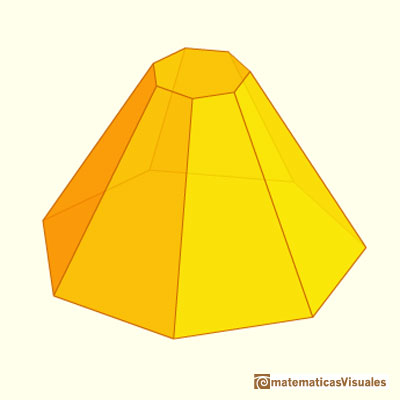

Como antes, necesitamos la altura de la cara lateral para calcular la superficie lateral de un tronco de pirámide:
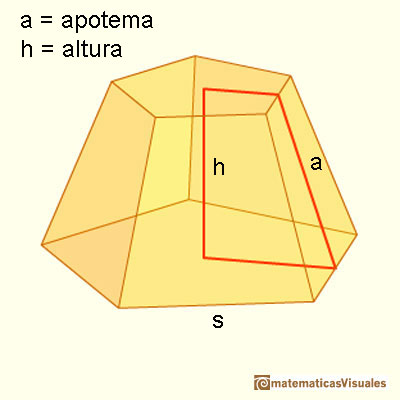
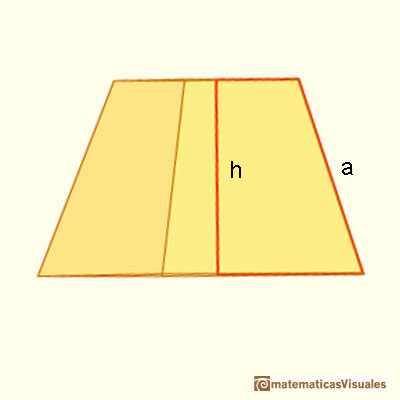
Si P es el perímetro de la base inferior y p el perímetro de la base superior, la fórmula de la superficie lateral es semejante a la fórmula del área de un trapecio (pues las caras laterales son trapecios congruentes):
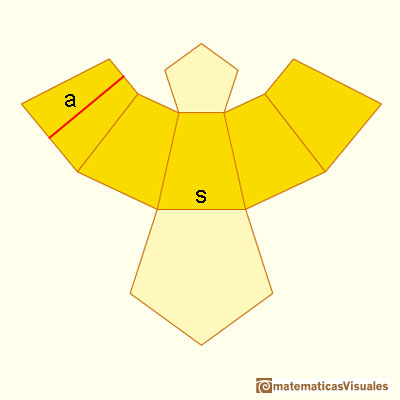
En los ejemplos anteriores las bases eran polígonos regulares. Podemos considerar pirámides cuyas bases no sean polígonos regulares. En el siguiente mathlet las bases no son regulares (aunque son polígonos que pueden inscribirse en una circunferencia y son polígonos convexos). Cada vez que modificamos el número de lados de la base se genera un nuevo polígono aleatoriamente.
 ANTERIOR
ANTERIOR
MÁS ENLACES
























 SIGUIENTE
SIGUIENTE