La figura formada cortando un cilindro circular infinito con dos planos se llama segmento cilíndrico o cilindro truncado. El caso más simple
es cuando uno de los planos corta al cilindro perpendicularmente al eje. Entonces el segmento cilíndrico tiene una base circular. Este es el caso
que vamos a estudiar aquí.
En esta página vamos a ver cómo un cilindro truncado se puede desarrollar en un plano.
Este es otro ejemplo:
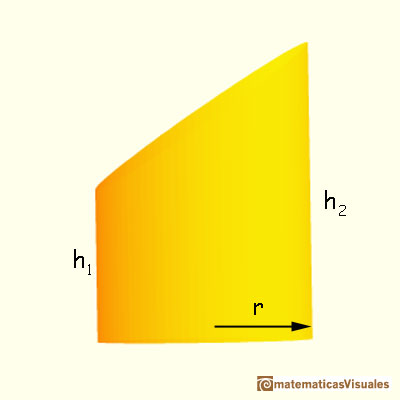
El volumen de un segmento cilíndrico se puede calcular fácilmente considerando dos copias del segmento cilíndrico, dándole la vuelta a una de ellas
y poniéndola encima. Entonces obtenemos un cilindro y ya podemos saber el área de la figura.
La sección de un cilindro por un plano oblicuo parece una elipse. De hecho es una elipse y lo podemos ver con una bonita demostración que usa las
esferas de Dandelin.
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
MÁS ENLACES
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
Desarrollos planos de pirámides truncadas por un plano oblicuo.
Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.
SIGUIENTE
ANTERIOR
