Hilber y Cohn-Vossen escribieron sobre el cilindro: "El cilindro circular es la superficie curva más sencilla. Se puede obtener a partir
de las curvas más simples -la línea recta y la circunferencia- moviendo una linea recta alrededor de una circunferencia manteniendola
perperdicular al plano del círculo. Otra manera de obtener el cilindro es rotando una recta alrededor de un eje paralelo a la recta.
Por lo tanto, el cilindro circular es una superficie de revolución. Las superficies de revolución son una clase de superficies importante
que se caracterizan por la propiedad de que pueden generarse rotando una curva plana alrededor de un eje que está en el mismo plano
de la curva."
(Hilber and Cohn-Vossen. Geometry and the Imagination. pag. 7).
En esta página, un cilindro está cerrado por dos planos paralelos perpendiculares al eje. Estos planos cortan al cilindro en dos círculos
que llamamos bases del cilindro.
El principal objetivo de esta página es mostrar cómo un cilindro puede desarrollarse en un plano.
La superficie lateral de un cilindro es el área de un rectángulo. La base de este rectángulo es la
longitud de la circunferencia de las bases. Podemos calcular la superficie lateral de un cilindro:
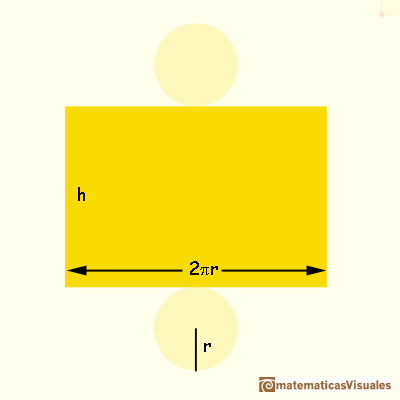
Para calcular la superficie total de un cilindro tenemos que sumar el área lateral y las áreas de los dos círculos de las bases. Entonces:
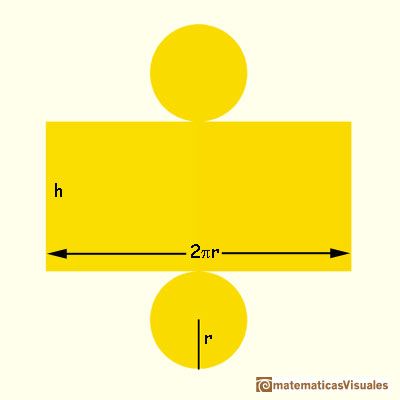
Recuerdas cómo se calcula el volumen de un cilindro?
MÁS ENLACES
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
Desarrollos planos de pirámides truncadas por un plano oblicuo.
Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera
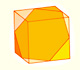
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.
Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.
SIGUIENTE
ANTERIOR
