Un cono es un cuerpo geométrico que consiste en una base plana cuya frontera es una curva cerrada (la directriz) y cada punto de esta curva está unido a un punto fijo (el vértice) que se encuentra fera del plano de la base. Una pirámide es un caso especial de cono con una base poligonal. Esa definición es demasiado general para nuestro propósito. El caso particular que vamos a tratar es cuando la directriz es una circunferencia y el vértice es un punto que se encuentra en la perpendicular desde el centro de es circunferencia. Decimos entonces que este cono es un cono circular recto. Un cono circular recto tiene simetria rotacional alrededor de la recta que pasa por el centro de la base y el vértice (y que es perpendicular a la base). Esta recta se llama eje del cono. Cada uno de los segmentos desde el vértice hasta un punto de la circunferencia de la base se llama generatriz del cono.
El principal interés de esta página es mostrar cómo los conos circulares rectos se pueden desarrollar en un plano. También veremos cómo se desarrollan los troncos de cono y calcularemos la superficie lateral y total de estas figuras.
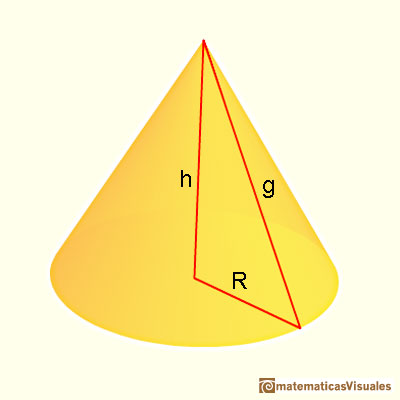
Este es un cono circular recto:

El cono desarrollándose en un plano:

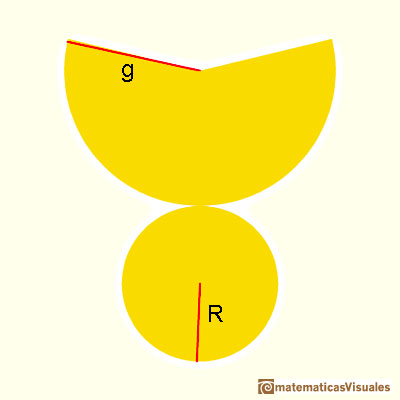
El cono completamente desarrollado en un plano, lo que llamamos desarrollo plano del cono:

Para calcular el área o superficie lateral de un cono necesitamos conocer la generatriz, es decir, la distancia entre el vértice y uno de los puntos de la circunferencia de la base. Hay una relación entre la generatriz y la altura del cono (por el teorema de Pitágoras)
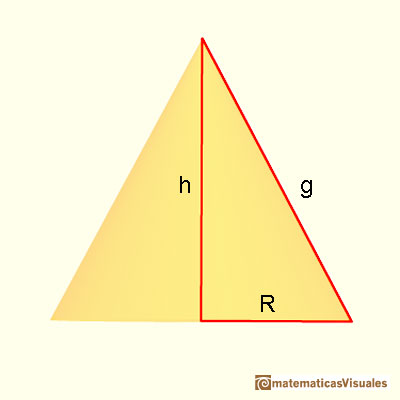
Vamos a calcuar la superficie lateral de un cono. Es el área de un sector circular. Si R es el radio de la base, la fórmula de la superficie lateral de un cono es semejante al área de un triángulo (Es un razonamiento intuitivo semejante al que hace Kepler en Kepler y el área del círculo):
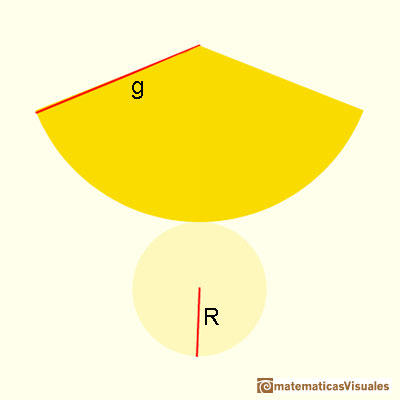
Si añadimos la superficie del círculo de la base obtenemos el área total del cono:
¿Recuerdas la fórmula del volumen de un cono?
Si cortamos un cono por un plano paralelo a la base obtenemos un cono truncado.
Este es un ejemplo de cono truncado:

que también se puede ir desarrollando en un plano:

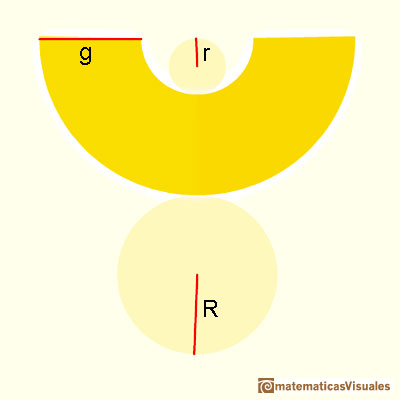
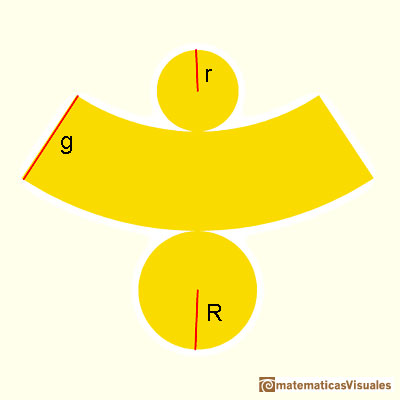
Este sería el desarrollo plano de un tronco de cono:

Como antes, necesitamos la generatriz para calcular la superficie lateral de un tronco de cono:
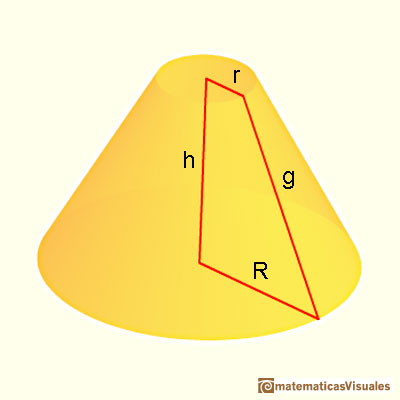
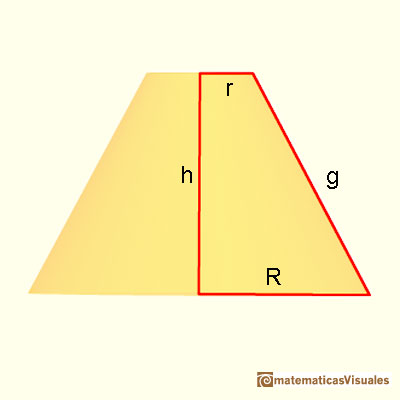
Podemos pensar, de un modo intuitivo, en que un tronco de cono es como un tronco de pirámide que tiene "infinitas caras laterales". Este modo impreciso de razonar nos puede recordar a los orígenes del calculo diferencial e integral, de la época de Kepler. Podemos recordar que la fórmula del área lateral de un tronco de pirámide era como la de un trapecio (las caras laterales son trapecios congruentes). Al calcular el área lateral de un tronco de cono ocurre algo análogo y la fórmula nos vuelve a recordar la del trapecio:
Puerta en Peñalba de Santiago (León, España) con un desarrollo de tronco de cono. Foto tomada en Julio de 2016.

MÁS ENLACES



























 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR