Truncar un poliedro significa que cortamos los vértices (o las aristas) de ese poliedro.
Ya hemos visto varios casos en los que hemos truncado los vértices de un poliedro regular.
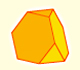
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
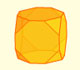
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.
En esta página vamos a ver el truncamiento de los lados de un cubo (achaflanar) y obtendremos un nuevo poliedro que vamos a llamar cubo achaflanado.
Podemos ver este achaflanamiento muchas veces pues se utiliza para rematar los cantos de muebles, encimeras de cocina, mármoles, etc.
Solemos usar una herramienta que se llama fresa para achaflanar piezas de diversos materiales.
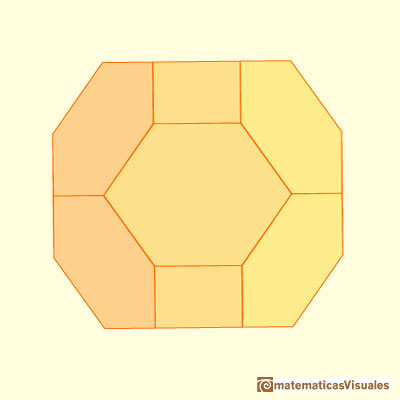
Achaflanado un cubo una determinada profundidad obtendremos un poliedro que tiene todas las aristas de igual longitud (equilátero). Tiene doce hexágonos que son equiláteros pero no equiángulos.
No son hexágonos regulares.
El cubo achaflando es un poliedro que es semejante al octaedro truncado. Sin embargo, el octaedro truncado tiene doce hexágonos regulares y es un sólido
arquimediano.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
Los hexágonos de un octaedro truncado son equiláteros y equiángulos.
Para comprobar que los hexágonos de un cubo achaflanado no tienen todos sus ángulos iguales vamos a calcular su medida. Para eso necesitaremos un poco de
trigonometría.
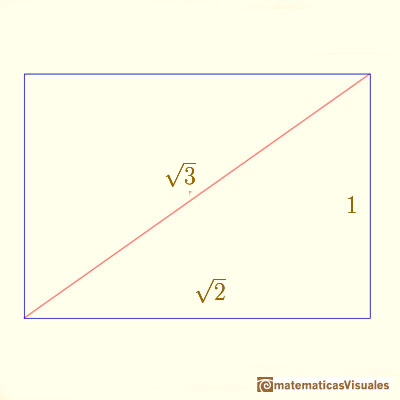
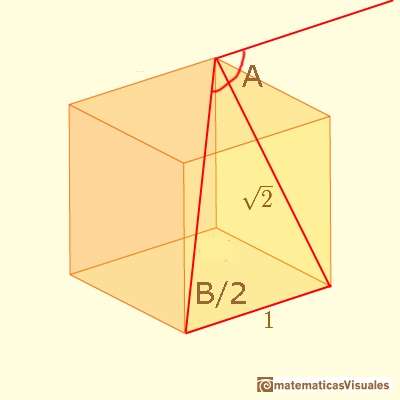
Los ángulos de este poliedro están relacionados con ángulos que ya encontramos cuando estudiamos el rectángulo DinA,
es decir, el rectángulo de las hojas de papel estandarizadas que usamos en muchas partes del mundo.
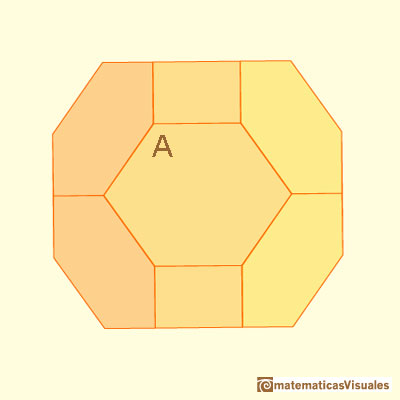
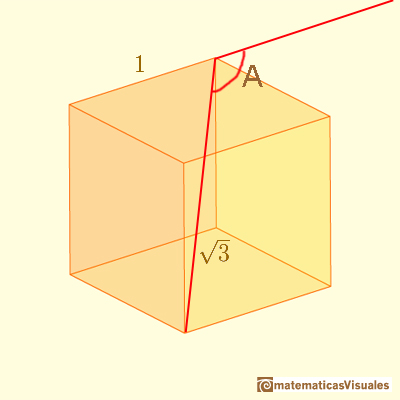
Podemos calcular el ángulo A:
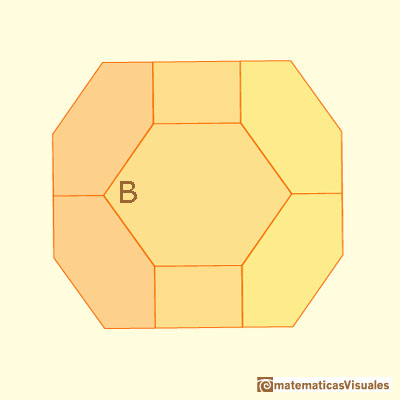
Entonces, el ángulo B:
De hecho
Como un caso límite podemos obtener un poliedro que tiene interesantes propiedades: el dodecaedro rómbico.
El dodecaedro rómbico y el cuboctaedro son poliedros duales.
El cubo achaflanado que tiene todas las aritas de igual longitud también se llama dodecaedro rómbico truncado pues lo podemos obtener
truncando los seis vértices de orden 4 de un dodecaedro rómbico de modo que esos vértices truncados sean cuadrados y los caras que eran rombos pasen a ser
hexágonos equiláteros (aunque no regulares).
MÁS ENLACES

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
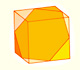
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro estrellado (que Kepler llamó stella octangula).








 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR





































