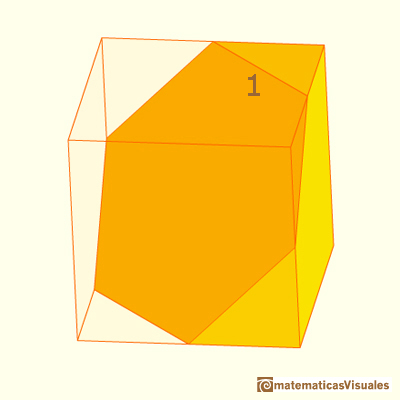
La intersección de un cubo por un plano perpendicular a una de sus diagonales por su centro es un hexágono regular.
Este plano divide al cubo en dos mitades.
En el Deutsches Museum, el Museo de Ciencias de Munich, podemos ver este modelo de la sección hexagonal de un cubo:
Este poliedro tiene propiedades interesantes. En esta página vamos a explorar dos de estas propiedades: La primera es que su volumen
es muy sencillo de calcular y la segunda es que este cuerpo tesela el espacio, es decir, que con este cuerpo podemos llenar el espacio sin
dejar huecos.
Para calcular el volumen podemos empezar calculando el volumen de un cubo cuando me dan la longitud de la diagonal de una cara.
Por ejemplo, si la diagonal tiene longitud 2 entonces el volumen lo podemos representar (calculando la longitud del lado):
Por lo tanto, el volumen de medio cubo:
La segunda propiedad es que este cuerpo rellena el espacio. También decimos que genera una teselación del espacio.
Esto está claro pues el cubo el el polyedro más sencillo que tesela el espacio y nuestro poliedro es solo medio cubo.
Esta propiedad tendrá interesantes consecuencias.
Con ocho de estos medios cubos podemos construir un octaedro truncado.
Esta relación entre el cubo y el octaedro truncado nos ayuda a comprender la propiedad de que el
octaedro truncado es un poliedro que tesela el espacio.
MÁS ENLACES

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.











 SIGUIENTE
SIGUIENTE



























