Un regular tetrahedron que tiene cuatro caras que son triángulos equiláteros,
cuatro vértices y seis aristas. Es un sólido platónico.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
Albert Durero fue el primero en publicar desarrollos planos de poliedros. En su libro
'Underweysung der Messung' ('Cuatro Libros de la Medida', publicado en 1525) el autor dibujó desarrollos planos de los cinco sólidos platónicos y de otros poliedros
(entre ellos, varios sólidos arquimedianos).
Por ejemplo, este tetraedro regular:
"[Durero] Él introdujo la técnica de representar información sobre objetos tridimensionales sobre una superficie plegando papel
en lo que en la actualidad llamamos una red. Este método implica el desarrollo de la superficie de un poliedro en una hoja
plana de papel de modo que la figura resultante se puede cortar en una sola pieza y plegar para formar un modelo
tridimensional del poliedro original". (Cromwell, p.127)
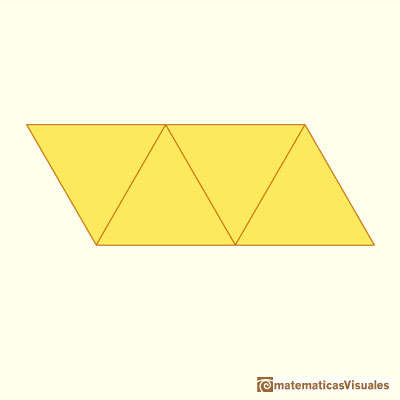
Jugando con la aplicación podemos ver cómo el tetraedro se desarrolla en su red plana. Este desarrollo plano del tetraedro
es muy típico, con la disposición de los cuatro triángulos equiláteros formando un triángulo equilátero mayor, cuya arista
es es doble que la del triángulo original. Este desarrollo es diferente del que dibujó Durero:
En el siguiente vídeo podemos ver el desarrollo plano tal como lo hizo Durero:
REFERENCIAS
Erwin Panofsky - The Life and Art of Albrecht Dürer - Princeton University Press
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press (p. 76)
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

Achaflanando un cubo, truncando sus aristas, podemos obtener un poliedro semejante (pero no igual) al octaedro truncado. También podemos obtener un dodecaedro rómbico.

Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.

Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.

Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
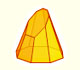
Desarrollos planos de pirámides truncadas por un plano oblicuo.

Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.
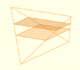
En su artículo 'Two Surprising Theorems on Cavallieri Congruence' (Dos teoremas sorprendentes sobre la congruencia de Cavalieri), Howard Eves describe un tetraedro muy interesante. En esta página calculamos las áreas de sus secciones y su volumen.

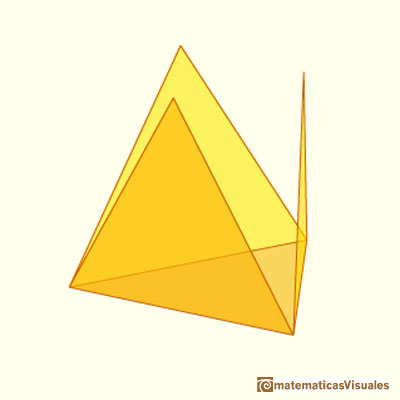
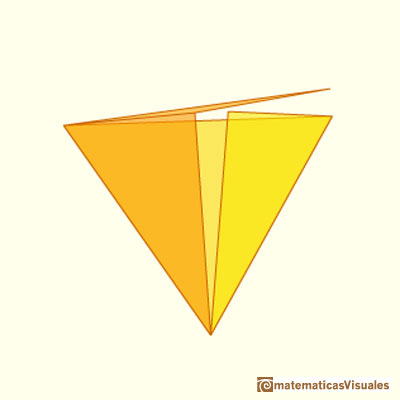
Haciendo adecuadamente secciones en un tetraedro obtenemos rectángulos y, en algún caso, un cuadrado. Podemos calcular el área de esas secciones.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.








 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR





























