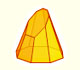
Conos cortados por planos oblicuos
En la página sobre conos truncados por un plano paralelo a la base hemos visto que estos cuerpos geométricos se pueden desarrollar en un plano.
El plano de sección puede no ser paralelo a la base, es lo que vamos a ver ahora.
El principal objetivo de esta página es mostrar cómo un cono cortado por un plano oblicuo puede desarrollarse en un plano.
Este es otro ejemplo:
SIGUIENTE
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.
ANTERIOR
Desarrollos planos de conos y troncos de cono. Cálculo del área lateral de estas figuras.
MÁS ENLACES
Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.
Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
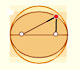
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
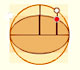
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.
En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.
El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
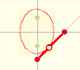
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.
Desarrollos planos de pirámides truncadas por un plano oblicuo.
Desarrollos planos de pirámides y de troncos de pirámide de base regular con diferentes números de lados.
Los cilindros son superficies de revolución que pueden desarrollarse en un plano. Se explica cómo calcular la superficie lateral y total de un cilindro.
Prismas con base regular o irregular cortados por un plano no paralelo a la base y sus desarrollos planos.
Estudiamos los prismas y vemos cómo se pueden desarrollar en un plano. Se explica el cálculo del área lateral de un prisma recto.