En esta página vamos a estudiar un instrumento mecánico que se usaba para dibujar elipses. Actualmente todavía se emplea para cortar elipses en diferentes materiales, por ejemplo, para hacer mesas elípticas.
Su nombre es "elipsógrafo" o "compás elíptico".
En inglés se conoce con el nombre de "Trammel" de Arquímedes. Es curioso investigar el origen de esta palabra. Su significado es "restricción", algo que impide una actividad, una limitación de la libertad. Está relacionada con red para pescar y proviene del latín. De su misma raíz es la palabra trasmallo (en aragonés, tresmallo) que utilizamos para nombrar una red para pescar (que puede ser que en su origen tuviera tres capas). Sorprendente evolución de una palabra que se usa en inglés para designar un aparato mecánico que dibuja elipses.
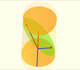
El siguiente dibujo es una representación clásica de este aparato que se puede ver en el libro 'Mathematical Models' de Cundy y Rollet.
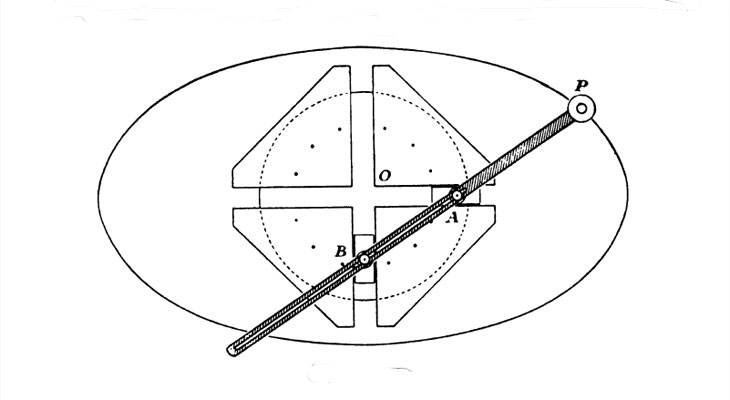
Este dispositivo mecánico se puede presentar de varias formas. Se trata de conseguir dos ranuras rectas y perpendiculares, lo que se puede hacer colocando sobre una base cuatro piezas triangulares o cuadrangulares. En estas ranuras se deslizan dos piezas que tienen fijada una varilla que puede girar conforme se desplazan las dos piezas sobre las ranuras.
El extremo de la varilla (de hecho, cualquier punto de la varilla) va a describir una elipse. Modificando la distancia entre los puntos de unión de la varilla con las piezas deslizantes obtenemos diferentes elipses.
Los dos deslizadores tienen los movimientos restringidos (de ahí la palabra 'trammel' en inglés) por las ranuras y al estar unidos a la varilla.
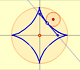
Lo que queremos comprobar es que el punto P describe una elipse.
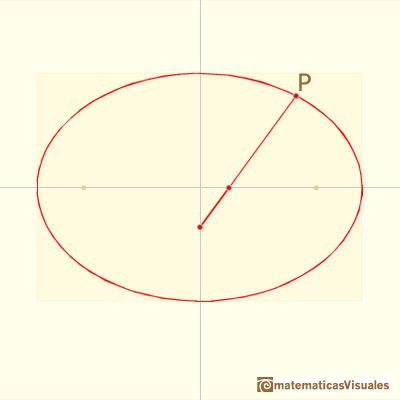
Ya sabemos algunas propiedades de la elipse que han sito tratadas en otras páginas de matemáticasVisuales.

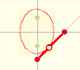
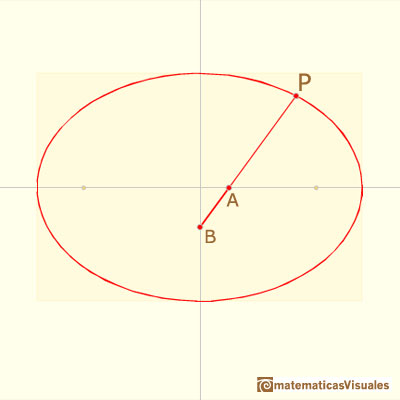
Para calcular las coordenadas del punto P usaremos esta notación y un poco de trigonometría:
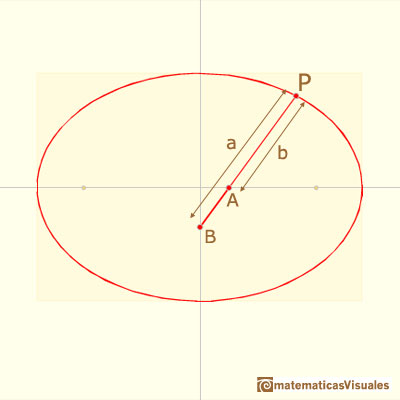
Entonces la coordenada X del punto es:
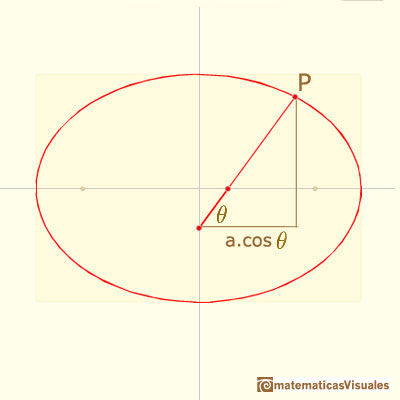
Y la coordenada Y del punto es:
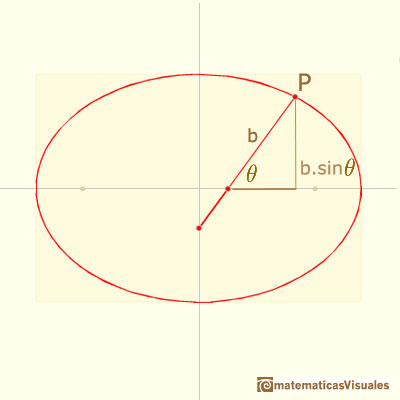
Las coordenadas del punto P son, por lo tanto:
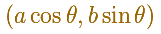
Sus coordenadas verifican la fórmula (en forma implícita) de la elipse:
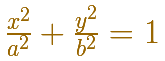
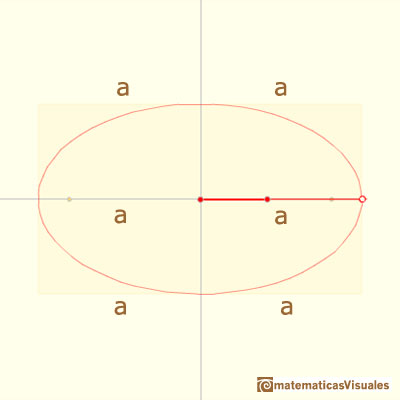
Los semiejes de el elipse son a y b, es decir, las distancias del extremo de la varilla y las dos piezas deslizantes.
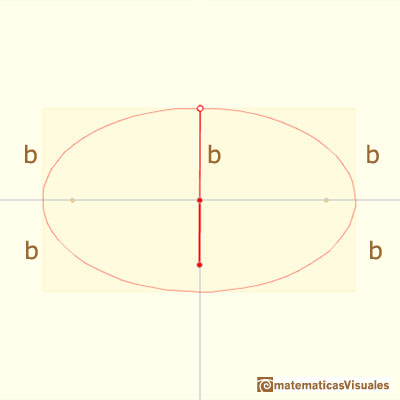
Modificando las distancias entre los puntos podemos obtener diferentes elipses:
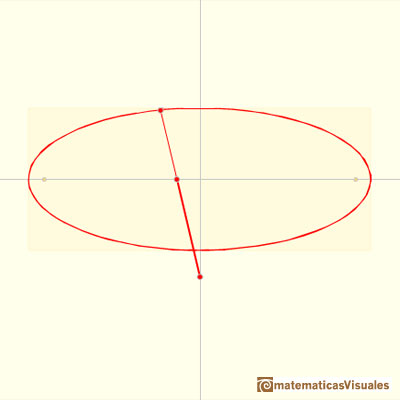
Este principio se usó para diseñar aparatos que dibujaran elipses que se llaman elipsógrafos.
El siguiente ejemplo pertenece a la colección del Museo Nacional de Ciencia y Tecnología, actualmente esta expuesto en el Museo Naval de Madrid y es el aparato que ha inspirado esta página:

Cualquier punto de la varilla describe una elipse, como puede verse en el siguiente video:
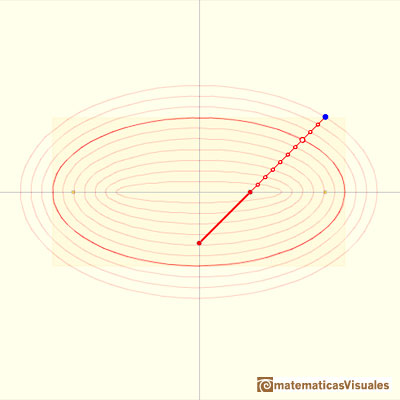
Cuando el punto P que dibuja se encuentra entre los dos puntos deslizantes también se generan elipses:
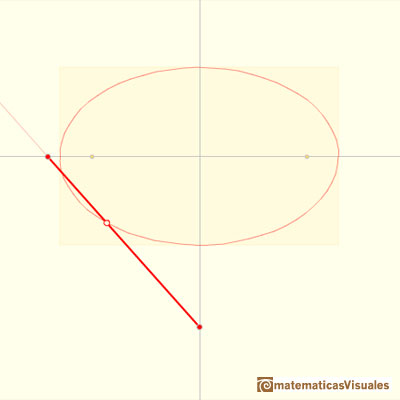

Incluso podemos dibujar una circunferencia como un caso particular de elipse:
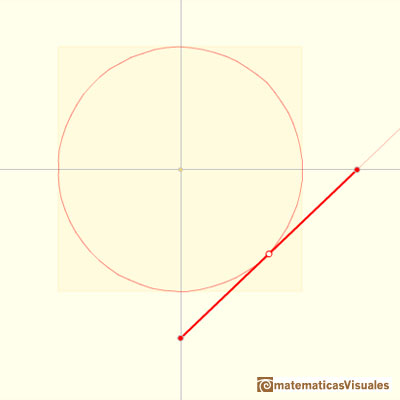
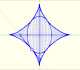
En próximas páginas estudiaremos estos casos, veremos que el segmento envuelve una curva que llamamos astroide y que tiene cuatro cúspides. La astroide aparece también como envolvente de las elipses y es un caso particular de hipocicloide.
En fin, que el elipsógrafo es un aparato que tiene mucho interés matemático y ha jugado su papel en la Historia de la Ciencia y la Técnica.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES