Ya hemos estudiado el elipsógrafo (o "trammel" de Arquímedes). Es un aparato que consite en una varilla que se mueve con dos puntos fijos
sobre dos rectas perpendiculares.

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
Los puntos de la varilla describen elipses.
También hemos considerado el segmento de longitud constante que se mueve con sus extremos sobre dos rectas perpendiculares.
Podemos ver este caso como el de una escalera que se desliza apoyada en el suelo y en una pared.
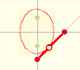
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
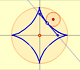
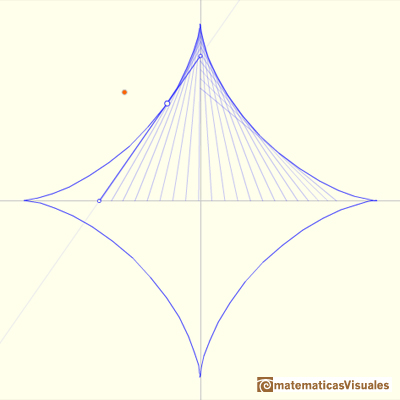
La envolvente de estos segmentos de longitud constante que se mueven con sus extremos sobre dos rectas perpendiculares es una
curva que tiene cuatro cúspides. Su nombre es astroide.
Podemos jugar con la primera aplicación interactiva para ver el segmento móvil y la astroide.
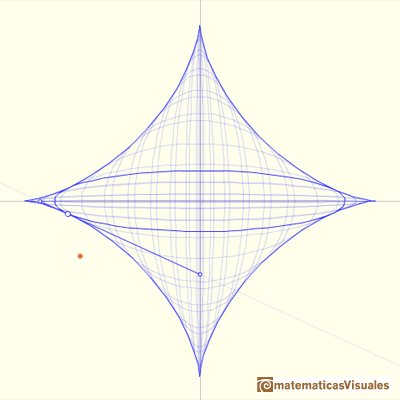
La astoide es también envolvente de una familia de elipses con la propiedad de que la suma de los ejes es constante
(la longitud del segmento móvil).
En este segundo vídeo podemos ver la astroide y la familia de elipses.
REFERENCIAS
Tom Apostol and Mamikon Mnatsakanian, 'New Horizons in Geometry' (Chapter 9. Trammels, ), Mathematical Association of America, 2012.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Hilbert and Cohn-Vossen, Geometry and the Imagination. Chelsea Publishing Company. pag.278.
Robert C. Yates, 'A Handbook on curves and their properties', J.W.Edwards-Ann Arbor, 1947.
J.L. Coolidge, The Mathematics of great Amateurs. Second Edition. Claredon Press. Oxford. Jan de Witt's proof in page 124.
MÁS ENLACES

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
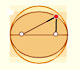
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.
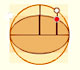
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.



 ANTERIOR
ANTERIOR



















 SIGUIENTE
SIGUIENTE