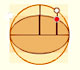
Arquímedes obtiene una elipse comprimiento una circunferencia en una dirección.
Entonces Arquímedes dedujo el área de una elipse como
una generalización del área del círculo.
Una elipse tiene dos ejes de simetría que llamamos el eje mayor y el eje menor.
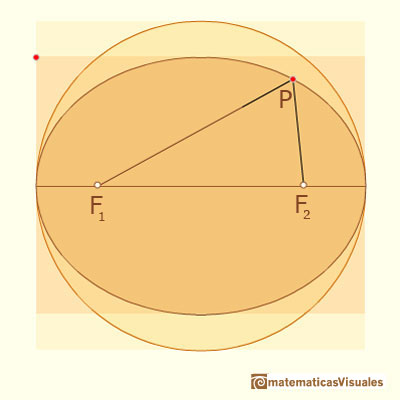
Una elipse se puede definir como el lugar geométrico de los puntos P tales que la suma de las distancias
desde P a dos puntos fijos F1 y F2 (llamados focos) es constante.
Estos dos focos están en el eje mayor a la misma distancia desde el centro de la elipse.
En esta página podemos ver (intuitivamente) como el enfoque de Arquímedes coincide con esta definición de una elipse.
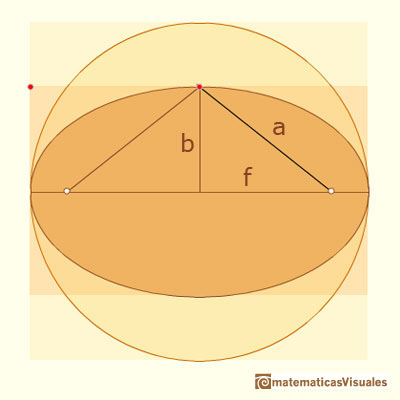
Podemos usar el teorema de Pitágoreas para calcular la posición de estos dos focos.
A partir de la definición, un punto P en la elipse verifica:
Una circunferencia es un caso especial de una elipse (cuando a = b). En este caso, los dos focos son el mismo punto: el centro de la circunferencia.
MÁS ENLACES

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Es un ejemplo de demostración rigurosa por doble reducción al absurdo.

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.
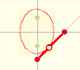
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.
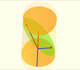
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
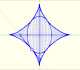
La astroide es la envolvente de un segmento de longitud constante cuyos extremos se mueven sobre dos rectas perpendiculares. También es la envolvente de una familia de elipses con la propiedad de que la suma de sus ejes es constante.
La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.

La sección de un cilindro por un plano es una elipse. Estas figuras se llaman segmentos cilíndricos o cilindros truncados y pueden desarrollarse en el plano.

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.
La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.

 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR