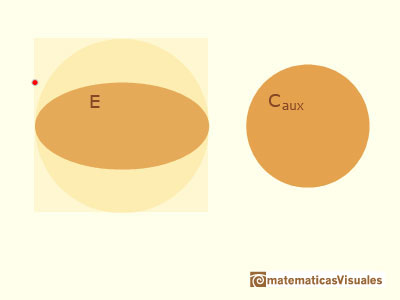
Conociendo el resultado, es decir, el área de la elipse, Arquímedes consideró un círculo secundario con la misma área que la elipse.

El radio de este círculo es:

Arquímedes quería probar que el área de la elipse es igual al área de este círculo secundario.

Arquímedes consideró un polígono similar a P', inscrito en el círculo auxiliar C'.

La relación entre las áreas de estos dos polígonos semejantes es:

Arquímedes comienza su doble reducción al absurdo.

Si fuera posible, sea el área del círculo secundario mayor que el ára de la elipse

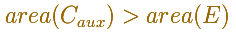
"Podemos entonces inscribir en el círculo secundario un polígono equilátero de 4n lados tal que su área es mayor que el de la elipse" [cf. De la esfera y el cilindro, I. 6.]" (Arquímedes)

Entonces

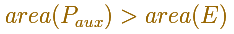
Entonces podemos consiederar un polígono similar en el círculo auxiliar y el correspondiente polígono en la elipse.

"Supongamos que P' denota el área de del polígono inscrito en el círculo auxiliar, y P el área del polígono inscrito en la elipse" (Archimedes)

Sabemos que

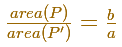
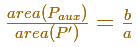
Entonces

"Pero esto es imposible, porque el primer polígono es por hipótesis mayor que la elipse, y, con mayor motivo, mayor que P.

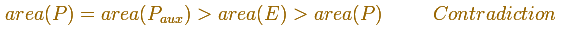
Por lo tanto el círculo secundario no es mayor que la elipse." (Arquímedes)

Si fuera posible, supongamos que el círculo secundario es menor que la elipse.

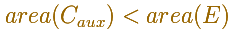
En este caso inscribimos en la elipse un polígono P con 4n lados iguales tal que

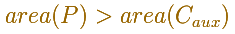
Arquímedes considera el polígono P' inscrito en el círculo auxiliar y un polígono semejante inscrito en el círculo secundario.

Como antes

lo cual es imposible.

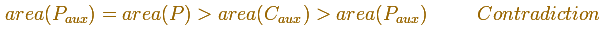
Esto completa la demostración por doble reducción al absurdo.

"Por lo tanto el círculo secundario, como no puede ser ni mayor ni menor que le elipse es igual a ella; y obtenemos el resultado requerido." (Arquímedes)

"En esencia, Arquímedes ha dado simplemente una prueba rigurosa por exhausción del hecho intuitivamente evidente de que el área de la elipse es b/a veces el área 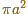de su círculo auxiliar, esto se corresponde con la observación de que el círculo se transofrma en la elipse comprimiendo su dimensión vertical por el factor b/a." (C. H. Edwards)

MÁS ENLACES

Desarrollos planos de cuerpos geométricos (8): Conos truncados por un plano oblicuo

Desarrollos planos de conos truncados por un plano oblicuo. La sección es una elipse.

Ecuación de la elipse

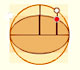
Transformando una circunferencia podemos obtener una elipse (como hizo Arquímedes para calcular su área). A partir de la ecuación de la circunferencia deducimos la de la elipse.

La elipse y sus focos

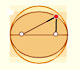
Una elipse tiene dos focos y la suma de las distancias de cualquier punto de la elipse a los dos focos es una constante.

Elipsógrafo: un aparato mecánico para dibujar elipses

El elipsógrafo es un aparato mecánico que se usa para dibujar elipses.

Elipsógrafo: un aparato mecánico para dibujar elipses (2)

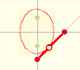
Si un segmento de longitud fija se mueve de modo que sus extremos están en dos rectas perpendiculares, cualquier punto del segmento traza una elipse.

Elipses como secciones de cilindros: Esferas de Dandelin

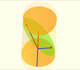
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

Alberto Durero y las elipses: secciones de un cono.

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Alberto Durero y las elipses: las elipses tienen dos ejes de simetría.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.

Astroide como envolvente de segmentos y elipses

La astroide es la envolvente de un segmento de longitud constante cuyos extremos se mueven sobre dos rectas perpendiculares. También es la envolvente de una familia de elipses con la propiedad de que la suma de sus ejes es constante.

La astroide es una hipocicloide

La astroide es un caso particular de una familia de curvas que llamamos hipocicloides.

El Método de Arquímedes para calcular el área de un segmento parabólico

Arquímedes explica en 'El Método' cómo se puede utilizar la ley de la palanca para descubrir cuál es el área de un segmento parabólico.

Kepler: El área de un círculo

Kepler usó una aproximación infinitesimal intuitiva para calcular el área de un círculo.

Durero y transformaciones

Durero estudió transformaciones aplicadas a figuras para, por ejemplo, modificar caras y generar otras caras o caricaturas. Algunas de estas transformaciones son afinidades.

La función coseno compleja

La función coseno compleja extiende la función real al plano complejo. Es una función periódica que comparte varias propiedades con la función real.