Ya hemos estudiado las secciones planas de un cilindro y sus desarrollos planos.

Sospechamos que la intersección de un cilindro y un plano (no paralelo al eje del cilindro) es una elipse.

En esta página vamos a probar este resultado usando una idea de debemos a Germinal Pierre Dandelin (1794-1847). Dandelin fue un matemático e ingeniero militar belga.
Ya sabemos muchas propiedades de las elipses. Una elipse se define habitualmente como el lugar geométrico de los puntos P tales que la suma de las distancias desde P a dos puntos fijos F1 y F2 (llamados focos) es constante. Usaremos esta defincición más adelante. [Tengo entendido que el primero en llamar a estos dos puntos fijos 'focos' fue Kepler quien afirmó que los planetas viajan alrededor del Sol siguiendo órbitas elípticas con el Sol en uno de los focos. Y foco proviene del latín 'focus' con un sentido original de hogar o fuego del hogar. Entonces foco significaría aquí lugar del que irradia luz o calor].
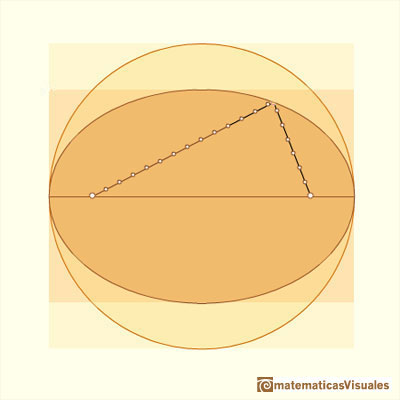
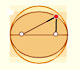
También sabemos cómo calcular el área de una elipse siguiendo a Arquímedes.

Incluso sabemos construir aparatos para dibujar elipses.
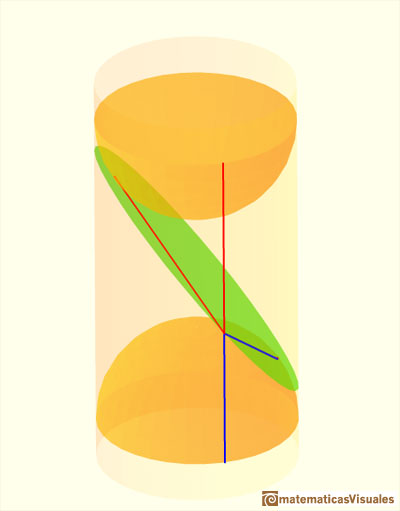
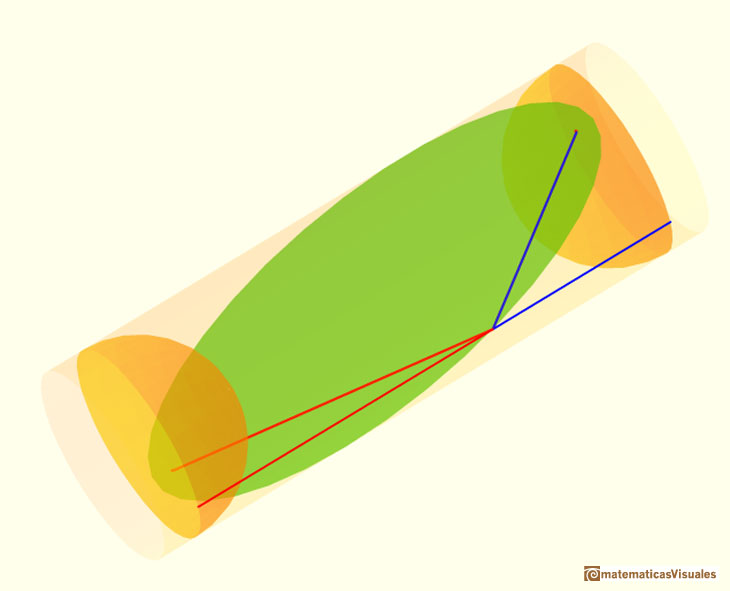
Para probar que la sección de un cilindro es una elipse Dandelin consideró dos esferas inscritas en el cilindro y tangentes al plano que corta al cilindro. Cada una de estas esferas es tangente al cilindro en una circunferencia. Estas circunferencias son paralelas y la distancia entre esas circunferencias a lo largo de cualquier generatriz del cilindro es constante.
Estas esferas se llaman Esferas de Dandelin.
También probaremos que los puntos de tangencia de las esferas con el plano son los focos de la elipse.
La aplicación interactiva nos permite cambiar la distancia entre las (semi)esferas, mover el punto sobre la elipse y rotar toda la figura para verla desde diferentes puntos de vista.
Vamos a seguir a Hilbert and Cohn-Vossen en su libro 'Geometry and the Imagination' para ver una demostración muy bonita de este hecho:
"Un cilindro circular corta a cualquier plano perpendicular a su eje en una circunferencia. Un plano que no sea perpendicular al eje ni paralelo interseca al cilindro en una curva que parece una elipse. Vamos a probar que esta curva es realmente una elipse. Para ello, consideramos una esfera que encaja en el cilindro y la movemos dentro del cilindro hasta que toque al plano (Fig. 9)."
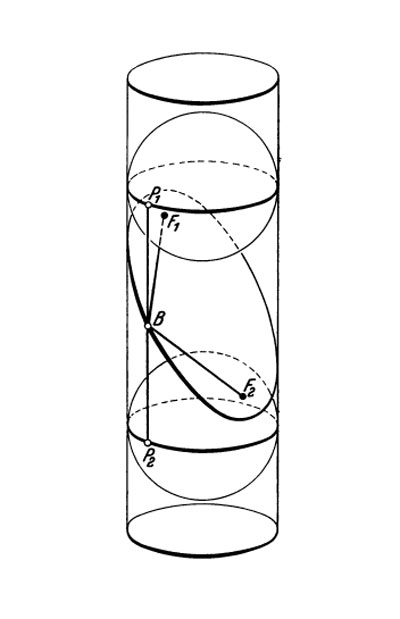
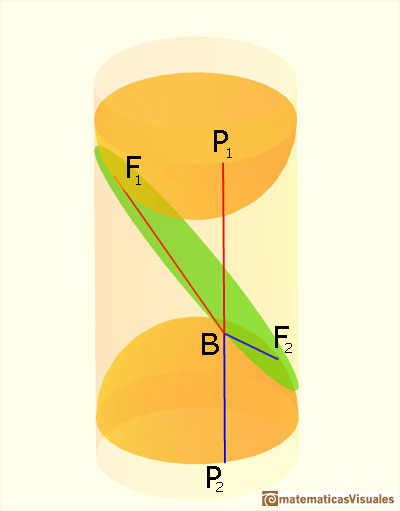

"Consideramos entonces otra esfera y hacemos lo mismo por el otro lado del plano. Las esferas tocan al cilindro en dos circunferencias y tocan al plano en dos puntos F1 y F2. Sea B otro punto cualquiera de la curva de interesección del plano con el cilindro. Consideramos la recta que pasa por B y que está en el cilindro (es decir, paralela al eje). Corta a las circunferencias de contacto de las esferas en dos puntos P1 y P2. BF1 y BP1 son tangentes a una esfera fija desde un punto fijo B, y todas estas tangentes deben ser iguales, debido a la simetria rotacional de la esfera. Por lo tanto BF1 = BP1; análogamente BF2 = BP2. Por lo tanto,
Por la simetria rotacional de nuestra figura, la distancia P1P2 es independiente del punto B de la curva. Por lo tanto BF1 + BF2 es constante para todos los puntos B de la sección, es decir, la curva es una elipse con focos F1 y F2."
"El hecho que acabamos de probar puede formularse en términos de la teoría de proyecciones como sigue: La sombra que hace una circunferencia sobre un plano oblicuo es una elipse si los rayos son perpendiculares al plano de la circunferencia." (Hilbert and Cohn-Vossen. Geometry and the Imagination)
Un caso particular de elipse es la circunferencia (los dos focos son el mismo punto al que llamamos centro de la circunferencia).






Si, en vez de cortar un cilindro, cortamos un cono nos encontramos en una situación más general. Las esferas de Dandelin nos sirven también en este caso para estudiar las secciones de un cono (no solo las elipses, también las parábolas y las hipérbolas).
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES