Durero fue matemático, además de pintor, dibujante y grabador. Vivió entre 1471 y 1528. Representante del
Renacimiento alemán. Se trata de la época de la Reforma. Vivió en Nuremberg y viajó por Italia y los Países
Bajos. Difundió las nuevas técnicas sobre perspectiva.
Escribió dos libros en alemán que tienen particular interés para las Matemáticas. El primero es un tratado en el que
estudia temas de Geometría útiles para artistas y artesanos ("Underweysung Underweysung der Messung", "Los cuatro libros de la medida").
En estos cuatro tomos podemos ver construcciones con regla y compás (exactas y aproximadas)
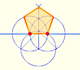
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
Posiblemente, fue el primero en publicar desarrollos planos de poliedros.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El segundo libro es "Los Cuatro Libros de las Proporciones Humanas" ("Vier Bücher von Menschlicher Proportionen").
Estos tomos también tienen interés matemático.
Se puede ver y descargar el libro en
Yale University Beinecke Rare Book and Manuscript Library.
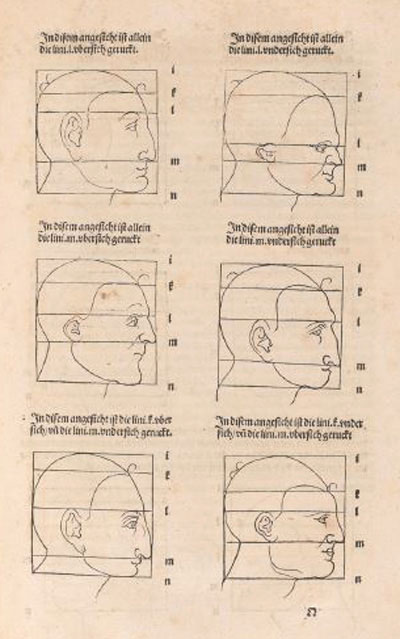
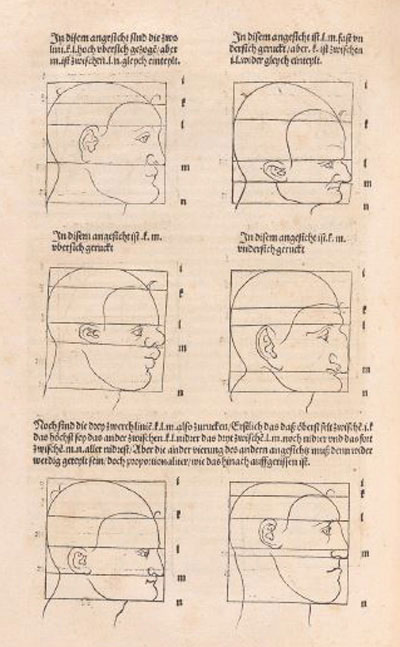
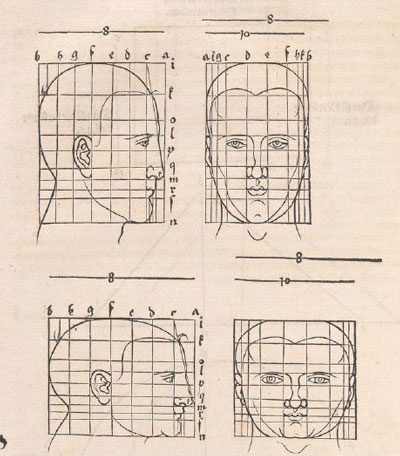
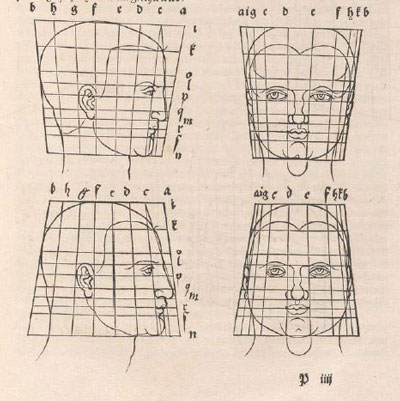
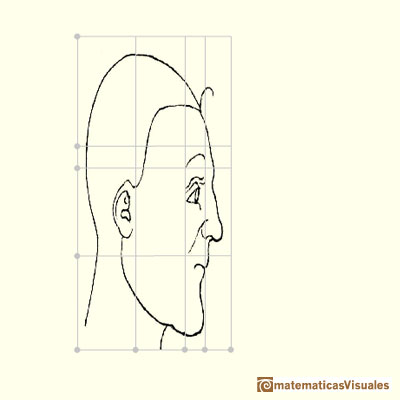
Durero describe métodos para cambiar las proporciones de las figuras, en particular, cabezas y caras.
Durero usaba cuadrículas rectilíneas en su dibujos. Esto no es nada nuevo pues este tipo de cuadrículas ya eran conocidas miles de años antes y
tenemos evidencias arqueológicas de los antiguos (por ejemplo, en Egipto) ya usaban este tipo de mallas en sus dibujos y esculturas.
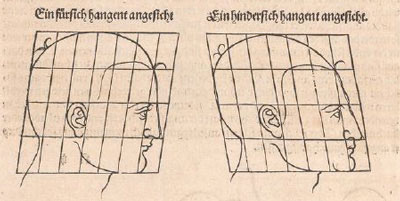
Pero Durero nos muestra una nueva idea pues transforma estas cuadrículas modificando al mismo tiempo la figura. Podemos decir que está usando
la cuadrícula como un primitivo "sistema de coordenadas".
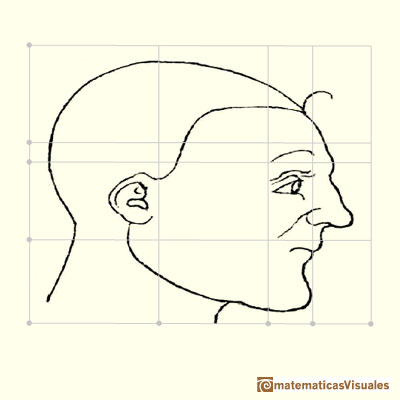
Se basó en transformaciones geométricas de diferentes tipos. Algunas de estas transformaciones las llamamos actualmente transformaciones afines.
Las transformaciones afines incluyen transformaciones como la compresión en una dirección.
Podemos usar este tipo de transformaciones para entender el método de Arquímedes para calcular el área de una elipse.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.
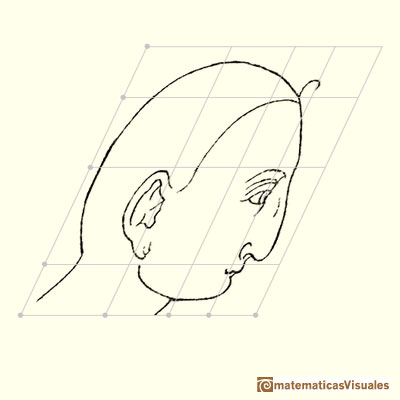
Otro tipo de transformación afín es una cizalla. En este caso se cambia el ángulo del sistema de coordenadas.
Las transformaciones afines son transformaciones lineales (las rectas se transforman en rectas) que preservan el paralelismo
(rectas paralelas se transforman en rectas paralelas).
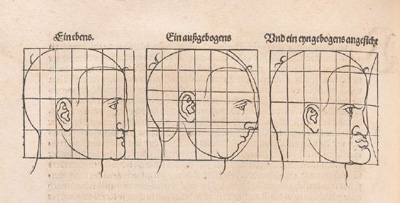
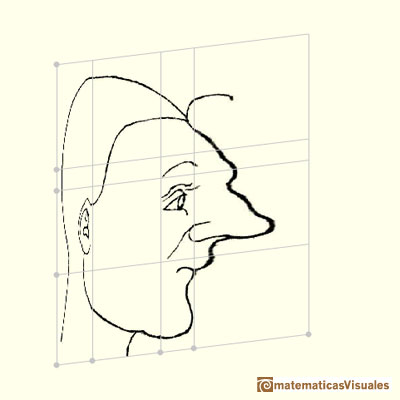
Además, Durero cambian diferentes zonas de la cuadrícula de modo diferente. Podemos decir que este tipo de transformaciones es una
tranformación afín "a trozos".
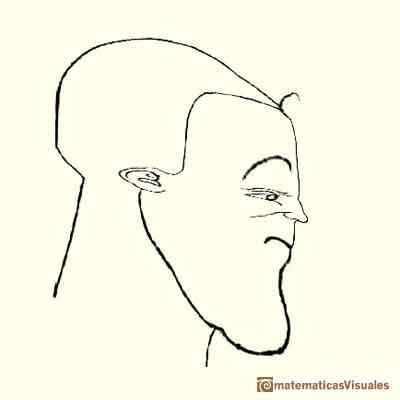
Con estas transformaciones "a trozos" obtiene caras deformadas como caricaturas, algunas veces grotescas.
MÁS ENLACES

Durero fue el primero en publicar en alemán un método para dibujar elipses como secciones de un cono.

Durero nos mostró un método excelente para dibujar elipses pero cometió un pequeño error. La intuición parece decirnos que la sección de un cono tiene forma de huevo. Podemos probar, usando conceptos básicos, que la elipse tiene dos ejes de simetría.
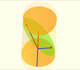
La sección de un cilindro por un plano que corta al eje del cilindro en un punto es una elipse. Probamos este resultado usando las esferas de Dandelin.

En su libro 'Sobre Conoides y Esferoides', Arquímedes calculó el área de la elipse. Podemos ver una aproximación intuitiva a las ideas de Arquímedes.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.
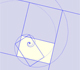
Un rectángulo áureo se descompone en un cuadrado y otro rectángulo áureo. Estos rectángulos están relacionados por una rotación dilatativa.

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.
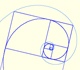
Dos espirales equiangulares contienen los vértices de rectángulos áureos.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
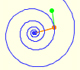
Cualquier dilatación de una espiral equiangular tiene el mismo efecto que una rotación.

En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
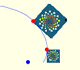
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.





 SIGUIENTE
SIGUIENTE