En la posición inicial del applet podemos ver una circunferencia. Cuando movemos el cursor vertical cambia la posición de una cuerda.
Queremos calcular el valor del segmento a cuando modificamos la posición vertical (x):
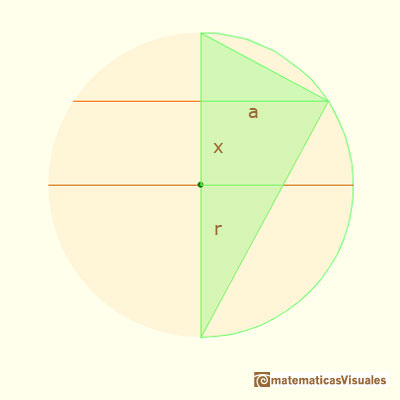
Nuestro objetivo es calcular la superficie de una sección de la esfera cuando cambiamos la distancia desde el centro de la esfera a la sección. Podemos ver la esfera pulsando y arrastrando sobre la esfera en el applet.
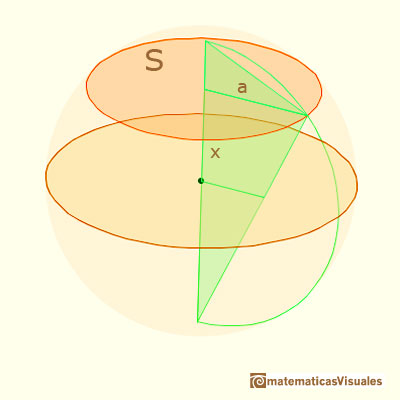
Usando el teorema de Pitágoras podemos calcular el radio de la sección:
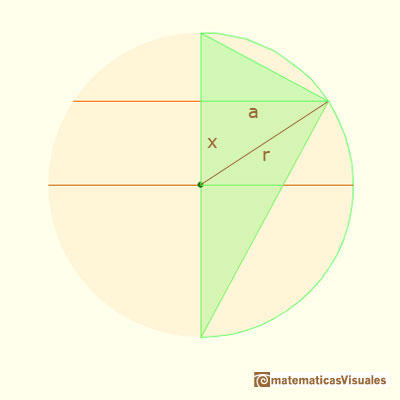
Entonces el área de la sección de la esfera es:

Ya hemos conseguido nuestro objetivo, pero podemos usar otro camino para calcular el radio a sin usar el teorema de Pitágoras. Podemos usar conceptos más básicos, como la semejanza de triángulos y, de paso, hablar de la media geométrica de dos números positivos.
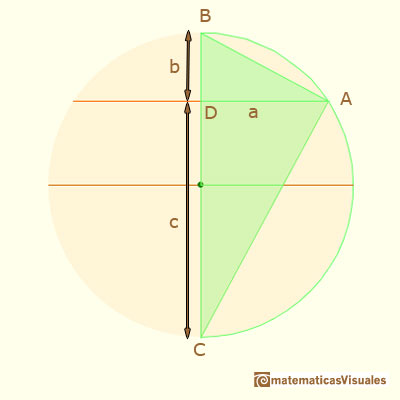
En la ilustración podemos ver tres triángulos rectángulos que son semejantes. Estamos interesados en dos de ellos:
Podemos escribir una proporción pensando en que queremos obtener el valor de a:
Entonces, el valor de a es:
Decimos que a es la media geométrica de dos números, b y c. Este resultado también se conoce como el Teorema de la altura de un triángulo rectángulo.
La media geométrica de dos números positivos está relacionada con la media aritmética:
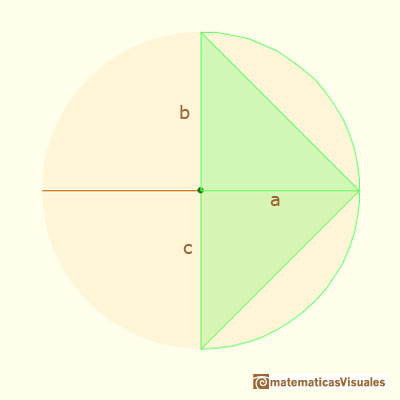
¿Puedes identificar qué segmento representa la media aritmética de dos números, b y c? ¿Cuándo son iguales la media aritmética y la geométrica?
Volviendo a nuestro objetivo inicial:
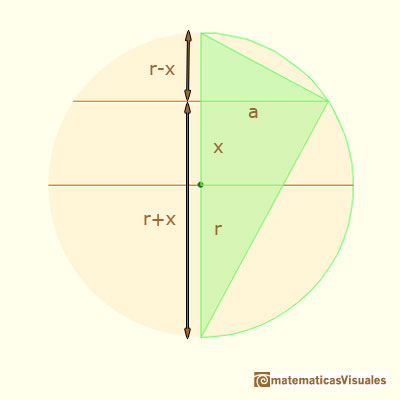
Vamos a usar este resultado en dos aplicaciones interesantes del Teorema de Cavalieri: Cómo calcular el volumen de una esfera y Two Surprising Theorems on Cavalieri Congruence (Dos teoremas sorprendentes sobre la Congruencia de Cavalieri). El primer resultado sorprendente que muestra Howard Eves en este artículo es que existe un tetraedro que tiene el mismo volumen que una esfera y que tienen las secciones correspondientes de la misma área. Aplicando el Teorema de Cavalieri se deduce el volumen de la esfera a partir del volumen del tetraedro.
Puedes jugar con estos dos applets para ver secciones en una esfera y casquetes esféricos:


REFERENCIAS
 SIGUIENTE
SIGUIENTE

 ANTERIOR
ANTERIOR
MÁS ENLACES