En MatemáticasVisuales ya hemos dedicado atención al teorema de Pitágoras y hemos podido jugar con aplicaciones interactivas que nos permiten 'ver'
demostraciones muy intuitivas de este famoso teorema. Una de ellas está inspirada en la demostración de Euclides (aunque Euclides no usa este
tipo de demostración dinámica pero los principios en los que se basan ambas demostración son muy parecidos). La otra está inspirada en un sencillo
mosaico.

Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.

Podemos ver el teorema de Pitágoras en un mosaico. Es una demostración gráfica sencilla del teorema de Pitágoras que vemos en suelos cuando se combinan cuadrados de dos tamaños.
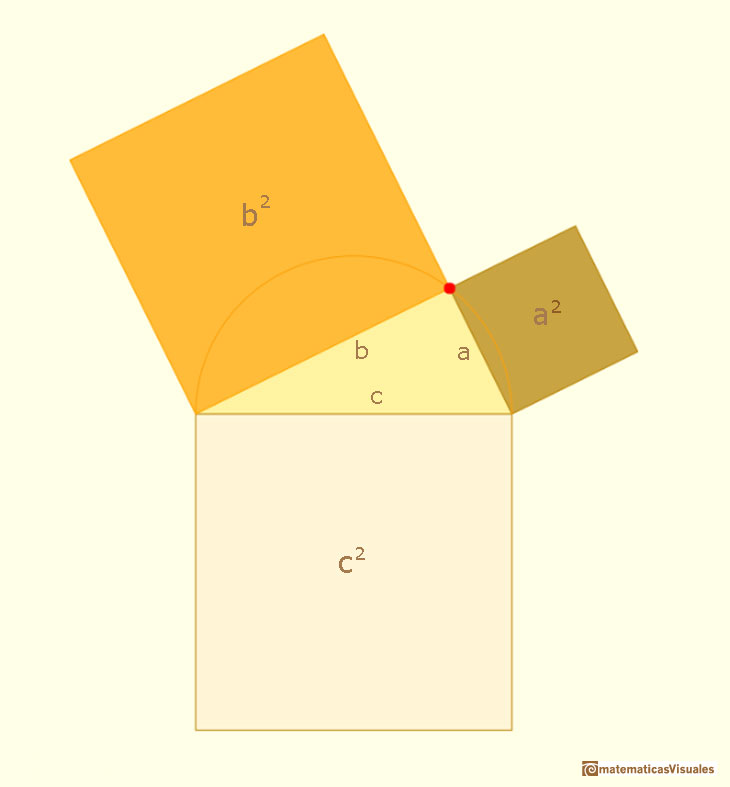
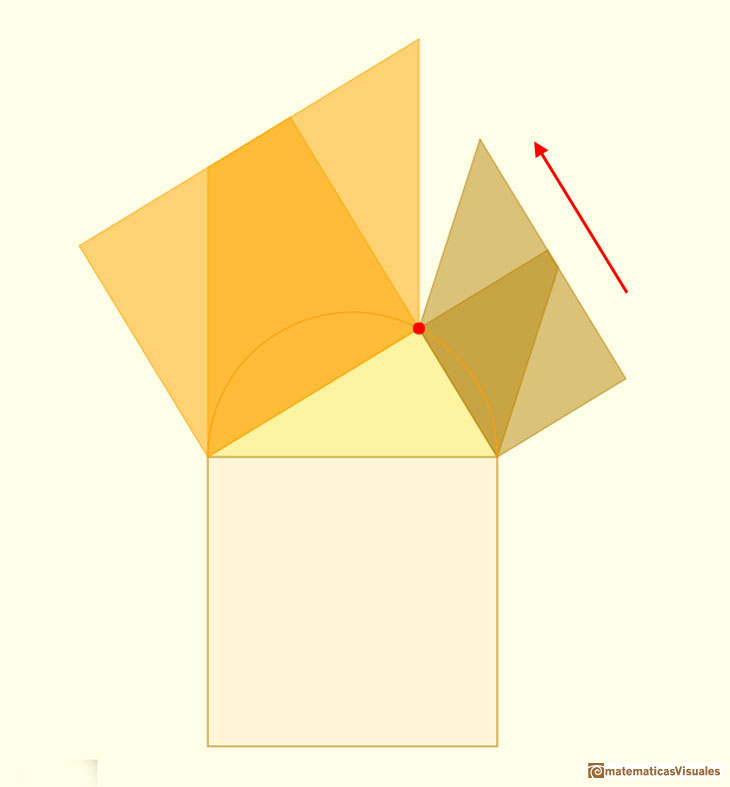
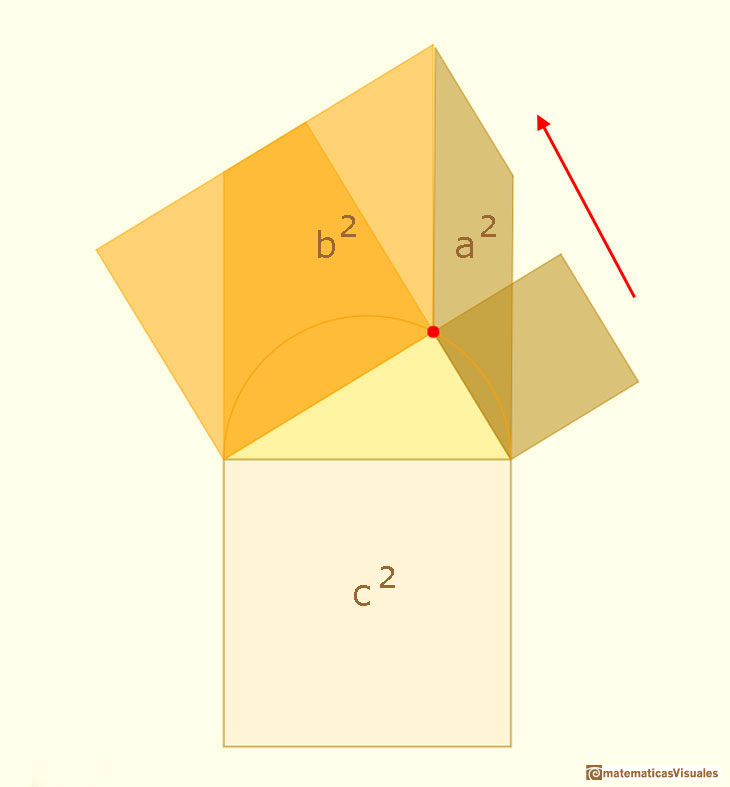
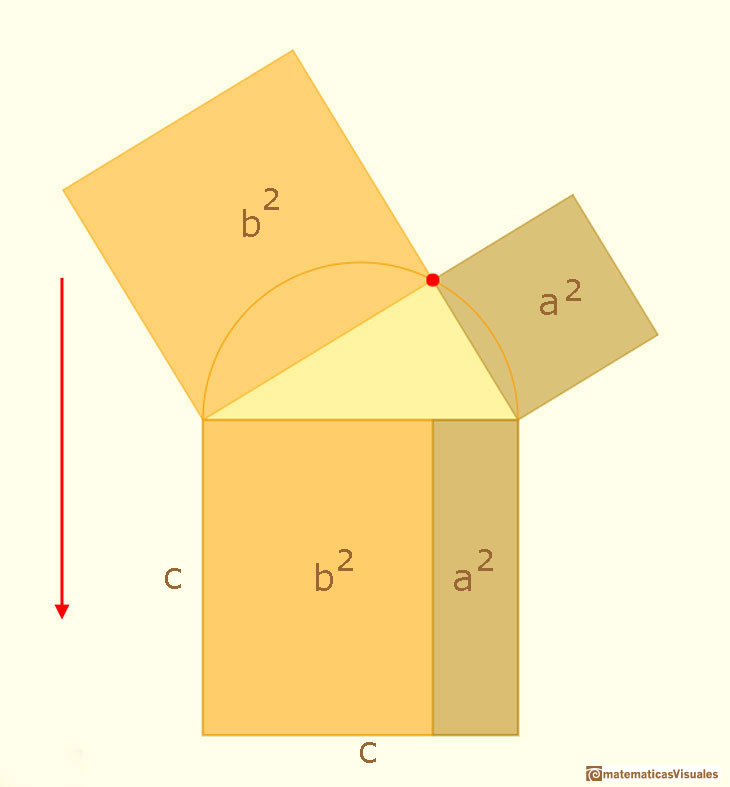
El teorema de Pitágoras trata de una importante propiedad de los triángulos rectángulos. Afirma que el (área del) cuadrado de la hipotenusa de un
triángulo rectángulo (el lado más largo) es igual a la suma de (las áreas de) los cuadrados de los dos catetos (los lados que forman el ángulo recto).
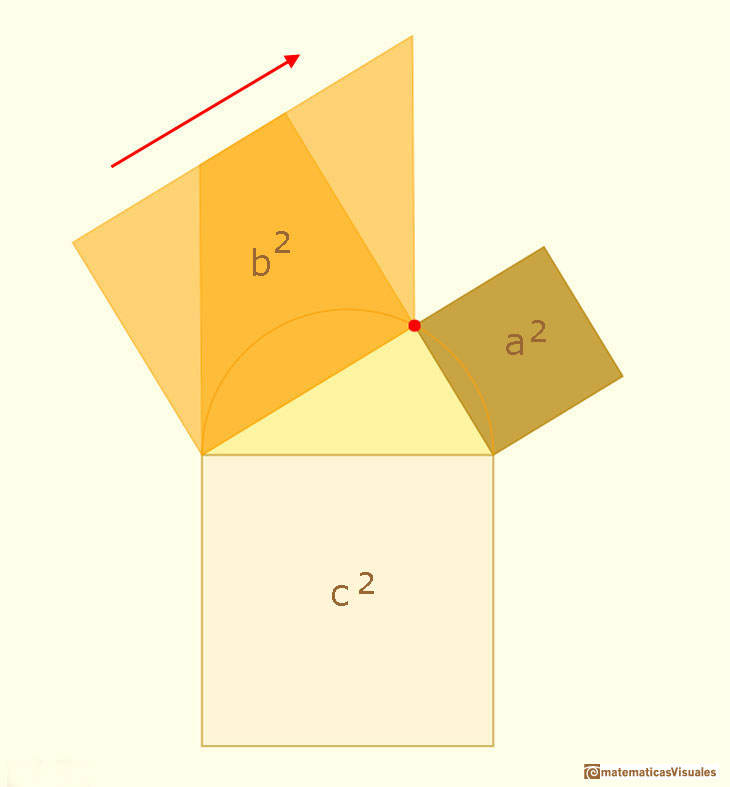
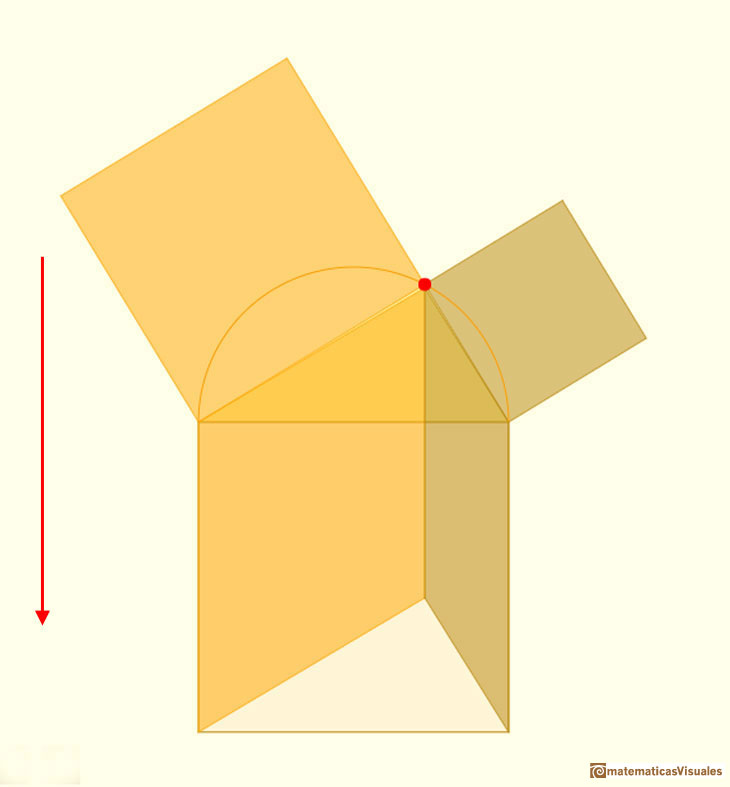
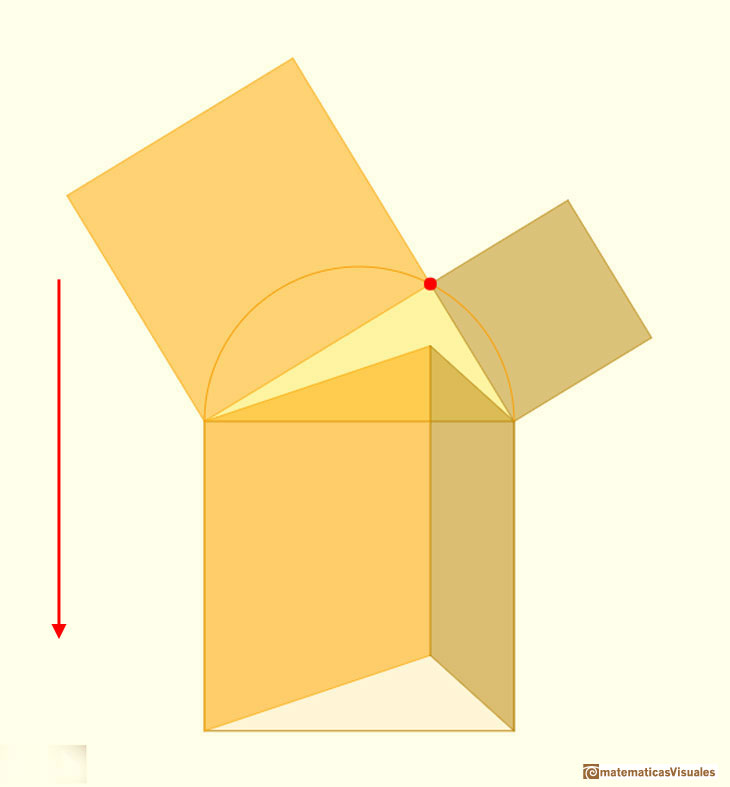
En esta página podemos interactuar con otra aplicación dinámica del teorema de Pitágoras que es la que hizo Hermann Baravalle (1945).
La principal idea es que si un paralelogramo se transforma por un cizallamiento (es decir, se transforma en un paralelogramo preservando la base y la altura)
su área permanece constante.
REFERENCIAS
Euclides, Los elementos
H.S.M. Coxeter, 'Introduction to Geometry', John Wiley and Sons, Second edition, pp. 8-9.
John Stillwell, "Mathematics and its History", Springer-Verlag, New York, 2002.
Martin Gardner, 'Sixth Book of Mathematical Diversions from "Scientific American"'. Scribner, 1975.
Eli Maor, "The Pythagorean theorem: a 4000-year history", Princeton University Press, United States of America, 2007.
F.J. Swetz and T.I. Kao, "Was Pythagoras chinese?", The Pennsylvania State University Press, United States of America, 1977.
MÁS ENLACES
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.

Calculamos el área de las secciones de una esfera usando el Teorema de Pitágoras. También estudiamos la relación con la media geométrica o el teorema de la altura de triángulos rectángulos.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
En su artículo 'Two Surprising Theorems on Cavallieri Congruence' (Dos teoremas sorprendentes sobre la congruencia de Cavalieri), Howard Eves describe un tetraedro muy interesante. En esta página calculamos las áreas de sus secciones y su volumen.

El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).

Estudiando el volumen de un barril, Kepler se planteó un problema de máximo en 1615.


 SIGUIENTE
SIGUIENTE























 ANTERIOR
ANTERIOR


