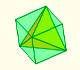
La construcción del compuesto de cinco tetraedros de modo que sus vértices estén en los veinte vértices de un dodecaedro regular es una preciosidad.
Estoy convencido de que todo aficionado a la construcción de poliedros se plantea hacerla en algún momento.
Hay varias técnicas para hacer esta construcción. En esta página vamos a ver varias de ellas. También se estudiarán algunas relaciones entre el dodecaedro, el cubo y el tetraedro que nos permitirán entender mejor esta figura.
En el vídeo se muestra mi último trabajo. Se trata de una combinación de la técnica de construcción usando vértices impresos con impresora 3d con tensegridad. Entiendo que es una construcción original y es la tercera que hago con esta combinación de técnicas (las otras dos son: icosaedro y cuboctaedro, tal como se pueden ver en la página de tensegridad. Un reto: ¿cómo se monta?.


La primera vez que vi esta construcción fue en 1982 cuando pude conseguir el libro 'Matemáticas más fáciles con manualidades de papel' que Ediciones Dístein publicó en 1975. Prácticamente, ya estaba agotada esta edición.

Este libro es la traducción de dos obras. La segunda parte es la traducción de 'Polyhedron Models for the Classroom' de Magnus J. Wenninger, uno de los expertos más reconocidos en construcción de poliedros.
Allí leí la técnica de copiar caras con ayuda de alfileres que describo en la página sobre construcción de modelos con cartulina.

Actualmente, esta técnica ya no es tan útil pues tenemos acceso a impresoras y fotocopiadoras.
Estas son las instrucciones que da Wenninger:
No es tan difícil de construir y el resultado es muy bonito. La fotografías no sustituyen la experiencia de manipular este modelo (como es habitual).

Podemos descargar el desarrollo de las piezas en el excelente sitio Korthalsates.
La técnica que yo usé fue construir todos los vértices usando un modelo semejante al primero de Korthalsates. Es decir, se pega la arista 'larga' con la cara para formar el vértice y el resto de las aristas tienen solapa. Después se van uniendo los vértices pegando solapa con solapa. Estas uniones quedan en el interior y dan mucha resistencia al modelo. Otros prefieren unir solapa con cara. Se pueden usar refuerzos interiores para alinear más correctamente algunas aristas de los tetraedros.
Años más tarde conocí el modelo realizado con origami modular. Se pueden ver las instrucciones de la construcción de cinco tetraedros en un dodecaedro. Una obra maestra del origami modular.


Para construir esta figura con Zome se necesitan las piezas verdes:


La misma construcción hecha con tubos de aluminio, tacos, hembrillas y bridas:
Usando tubos de plástico de colores unidos con vértices impresos con impresora 3d se obtiene una figura muy vistosa.
Si con gomas elásticas unimos los vértices obtenemos una tensegridad.


La belleza de estas figuras salta a la vista. Pero ¿cómo se puede justificar la estructura?¿Qué enseñanzas matemáticas podemos obtener de su construcción?
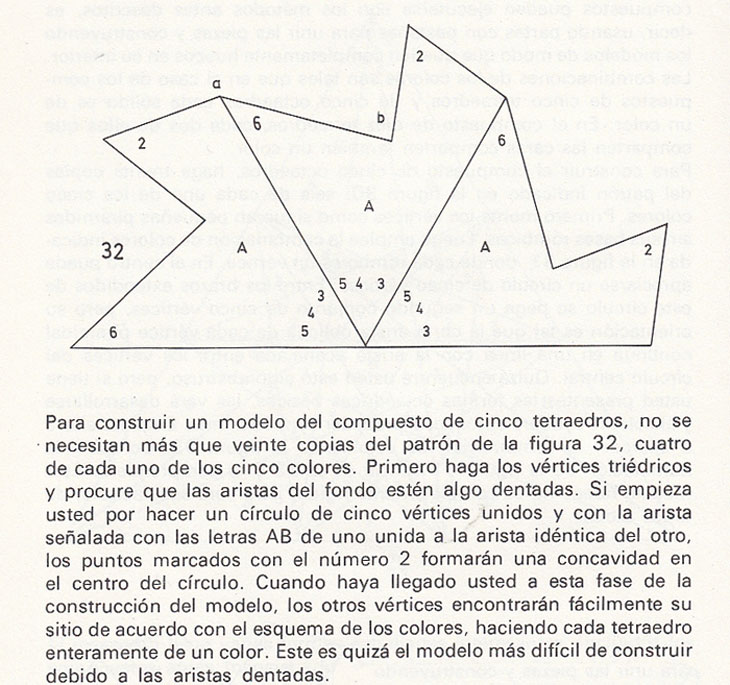
La clave está en que dentro del dodecaedro podemos inscribir un cubo. Dicho de otra manera, un dodecaedro puede verse como un cubo al que hemos añadido seis 'tejadillos'.
Este hecho era conocido por Euclides (Proposición 17 del Libro XIII de los 'Elementos') y fue dibujada por Kepler en su libro 'Harmonices Mundi':

Esta construcción es, desde luego, muy interesante. Una de sus consecuencias es que nos permite calcular el volumen del dodecaedro de un modo bastante sencillo:

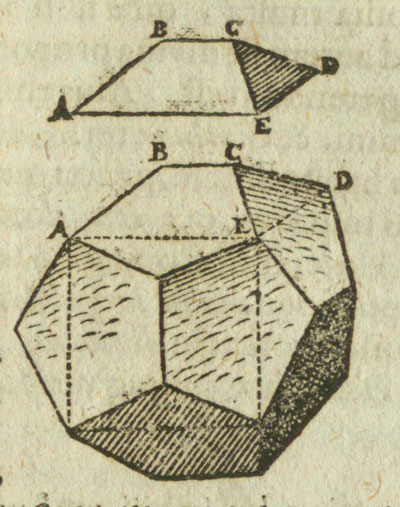
Inscrito en el cubo podemos poner un tetraedro:
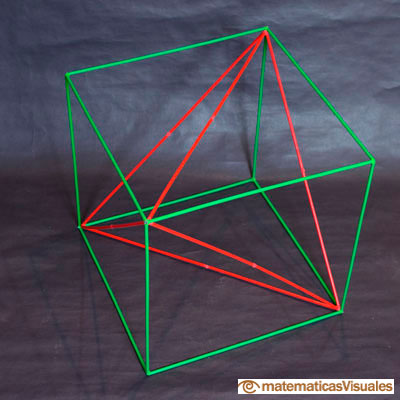
La siguiente imagen muestra un dodecaedro con un cubo inscrito que tiene, a su vez, un tetraedro inscrito (usando Zome):

Un tetraedro inscrito en un dodecaedro (usando Zome):

Si nos fijamos en esta relación entre el dodecaedro, el cubo y el tetraedro podemos calcular la longitud de la arista del tetraedro inscrito en un dodecaedro de arista unidad:
Cada arista del cubo es una diagonal de una cara pentagonal del dodecaedro. Luego podremos poner cinco cubos en un dodecaedro y, en cada cubo, un tetraedro. Así obtendremos nuestra figura de cinco tetraedros en un dodecaedro.
Se puede construir esta preciosa figura del compuesto de cinco cubos inscritos en un dodecaedro:


Este precioso modelo fue publicado por Tarquin hace muchos años y todavía puede adquirirse. El título es Advanced Polyhedra 3: The Compound of Five Cubes'. Muy recomendable.
Para terminar, podemos decir que inscrito en cada cubo se pueden colocar dos tetraedros inscritos. Estos dos tetraedros se cruzan y están en 'posición recíproca'. Forman la figura bien conocida desde tiempo inmemorial y que Kepler bautizó como stella octangula.

Los cinco tetraedros en un dodecaedro se pueden colocar de dos maneras distntas. Obtenemos dos poliedros simétricos no superponibles. Podemos decir que son dos formas quirales o enantiomorfas, una dextrogira y otra levógira.

Combinando estas dos figuras, o lo que es lo mismo, colocando dos tetraedros en cada uno de los cinco cubos que se pueden inscribir en un dodecaedro, obtenemos una preciosa y compleja figura que es el compuesto de diex tetraedros en un dodecaedro.
La siguiente página se dedica al estudio de este compuesto de diez tetraedros:
Arturo Soria y el Pentatetraedro
Arturo Soria (1844-1920), promotor de la Ciudad Lineal en Madrid, fue una persona con muchos intereses. Fue un gran aficionado al estudio de los poliedros y pensó que era el descubridor de este compuesto de cinco tetraedros que él llamó Pentatetraedro.
Aunque este compuesto ya había sido descrito con anterioridad eso no le quita mérito a Arturo Soria y él estaba muy orgulloso de su descubrimiento. Construyó modelos de las dos versiones de este poliedro y del compuesto de diez tetraedros, entre otros muchos modelos.
El Museo de Historia de Madrid se expone (hasta el 19 de Junio de 2022) 'Arturo Soria. Una mente poliédrica'.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES