Ya hemos visto, en la página dedicada al estudio del compuesto de cinco tetraedros, que
se pueden colocar cinco tetraedros inscritos en un dodecaedro de dos formas distintas.

Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
Obtenemos así dos formas de este poliedro simétricas no superponibles. Decimos que son dos formas quirales o enantiomorfas.
Podemos considerar una de ellas dextrogira y la otra, levógira.
Si combinamos estas dos construcciones sobre el mismo dodecaedro obtenemos el compuesto de diez tetraedros:
Este precioso modelo está comentado en los libros de Wenninger y en el de Cundy y Rollet. Esta es la imagen del libro de Cundy y Rollet:
Diez tetraedros (del libro 'Mathematical Models', de Cundy y Rollet)
Repasamos una justificación de esta construcción.
La clave está en que dentro del dodecaedro podemos inscribir un cubo. Dicho de otra manera, un dodecaedro puede verse como
un cubo al que hemos añadido seis 'tejadillos'.
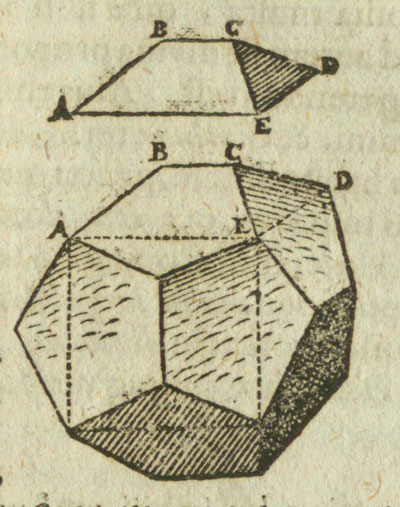
Este hecho era conocido por Euclides (Proposición 17 del Libro XIII de los 'Elementos') y fue dibujada por Kepler en su libro
'Harmonices Mundi':

Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
Como consecuencia, podemos inscribir cinco cubos en un dodecaedro de modo que cada arista del cubo sea una diagonal de una
cara pentagonal del dodecaedro:
Se puede construir esta preciosa figura del compuesto de cinco cubos inscritos en un dodecaedro
(modelo publicado por Tarquin):
Por otra parte, podemos inscribir un tetraedro en un cubo:

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
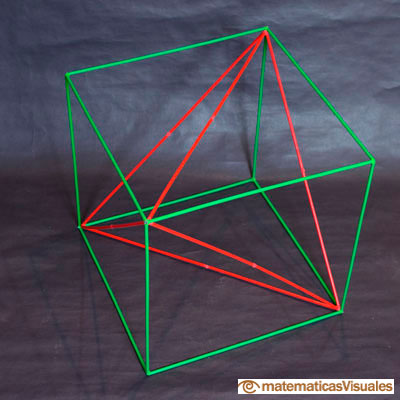
La siguiente imagen muestra un dodecaedro con un cubo inscrito que tiene, a su vez, un tetraedro inscrito (usando Zome):
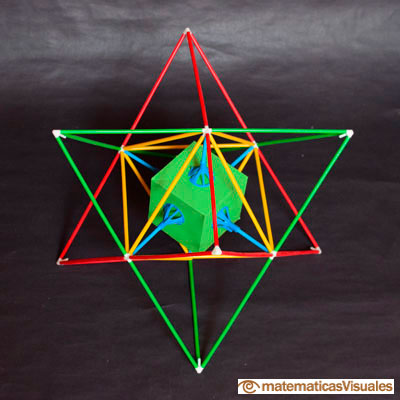
Pero en cada cubo se pueden colocar no uno sino dos tetraedros inscritos. Estos dos tetraedros se
cruzan y están en 'posición recíproca'. Forman la figura bien conocida desde tiempo inmemorial y que Kepler bautizó como
stella octangula.

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.
Si en un dodecaedro regular inscribimos cinco cubos y en cada cubo inscribimos dos tetraedros, estos diez tetraedros
forman el compuesto que estamos estudiando.
Es combinación de las dos formas quirales del compuesto de cinco tetraedros.

Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.
Es interesante notar que los compuestos de cinco tetraedros tienen veinte caras. Al combinar las dos formas compuestas de cinco tetraedros
resulta que los planos que contienen sus caras coinciden dos a dos.
Es decir, el compuesto de diez tetraedros tiene veinte caras.
Arturo Soria, el Pentatetraedro y el compuesto de diez tetraedros.
Arturo Soria (1844-1920), promotor de la Ciudad Lineal en Madrid, fue una persona con muchos intereses. Fue un gran aficionado al
estudio de los poliedros y pensó que era el descubridor del compuesto de cinco tetraedros que él llamó Pentatetraedro.
Aunque este compuesto ya había sido descrito con anterioridad eso no le quita mérito a Arturo Soria y él estaba muy orgulloso de
su descubrimiento. Construyó modelos de las dos formas quirales de este poliedro y también del compuesto de diez tetraedros,
entre otros muchos modelos.
El Museo de Historia de Madrid se expone (hasta el 19 de Junio de 2022) 'Arturo Soria. Una mente poliédrica'.
REFERENCIAS
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Se puede inscribir un cubo en un dodecaedro y podemos ver el dodecaedro como un cubo con seis 'tejados' añadidos uno en cada cara. Estos seis tejados del dodecaedro se pueden plegar en un cubo.

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
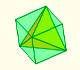
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.

Añadiendo cuatro tetraedros a un octaedro podemos obtener un tetraedro. Calculamos el volumen de un tetraedro a partir del volumen de un octaedro y usando semejanza.

Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.













 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
































