Esta página es complementaria de la exposición: "Los sólidos platónicos" que se realizó en el IES Alonso Quijano de Alcalá de Henares durante los meses mayo y junio de 2021 y que también se ha expuesto en el IES Atenea de Alcalá de Henares, el IES Gaspar Sanz de Meco, el IESO Harévolar de Alovera (Guadalajara) y el IES Ignacio Ellacuría de Alcalá de Henares.

Esta exposición es la segunda de una serie de tres que se realizaron en el IES Alonso Quijano entre los años 2020 y 2022.

El IES Ignacio Ellacuría de Alcalá de Henares es el quinto instituto en acoger la exposición 'Los sólidos platónicos'. La inauguración coincide con el Día Internacional de las Matemáticas, es decir, el 14 de marzo y estará hasta mayo de 2023. Muchas gracias a los profesores del Departamento de Matemáticas por su interés y colaboración.

El cuarto instituto en acoger la exposición 'Los sólidos platónicos' es el IESO Harévolar de Alovera (Guadalajara). Estuvo durante los meses de marzo y abril de 2022. Muchas gracias a las profesoras que han colaborado en la instalación.

La exposición 'Los sólidos platónicos' se ha trasladado al IES Gaspar Sanz de Meco durante los meses de enero y febrero de 2022. Gracias al Departamento de Matemáticas del IES Gaspar Sanz.

La exposición 'Los sólidos platónicos' se ha trasladado al IES Atenea de Alcalá de Henares durante los meses de noviembre y diciembre de 2021. Ahora más alumnos podrán aprovecharla. Esto ha sido posible gracias al interés del Departamento de Matemáticas del IES Atenea.

En la exposición se muestran diferentes construcciones de los cinco sólidos platónicos (o poliedros regulares) realizadas con cartulina y con varillas.

Las aristas de esos poliedros realizados en cartulina son iguales. Se aprecia el diferente volumen.

Los mismos poliedros se han construido con varillas de plástico. Esto destaca los vértices y las aristas de los poliedros. Se ha señalado una de sus caras.

Se asocia a cada poliedro un elemento, tal como describe Platón en su libro "Timeo".

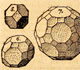
Esta es una representación antigua de estos cinco poliedros en el libro de Kepler (1571-1630) "Harmonices Mundi" ("La harmonía del mundo"). En esta ilustración se muestran los poliedros y su asociación con los cuatro elementos. El tetraedro con el fuego, el octaedro con el aire, el cubo con la tierra y el icosaedro con el agua. El dodecaedro estaría asociado con el universo o cosmos.

Cinco cuadros representan esta asociación entre los sólidos platónicos y los elementos:

El tetraedro asociado con el fuego:

El octaedro asociado con el aire:

El cubo asociado con la tierra:

El icosaedro asociado con el agua:

El dodecaedro asociado con el cosmos:

Estos cinco sólidos se van a ir emparejando. En cada pareja, uno está dentro del otro.

El icosaedro dentro del octaedro.

El octaedro dentro del tetraedro.

El tetraedro dentro del cubo.

El cubo dentro del dodecaedro.

La exposición culmina con dos estructuras en la que se muestran los cinco sólidos platónicos encajados.

Veremos que hay dos maneras típicas de hacer este tipo de construcciones. En la exposición se muestran las dos. Fundamentalmente se diferencian en la colocación del icosaedro.

La más grande se corresponde con el emparejamiento descrito más arriba.

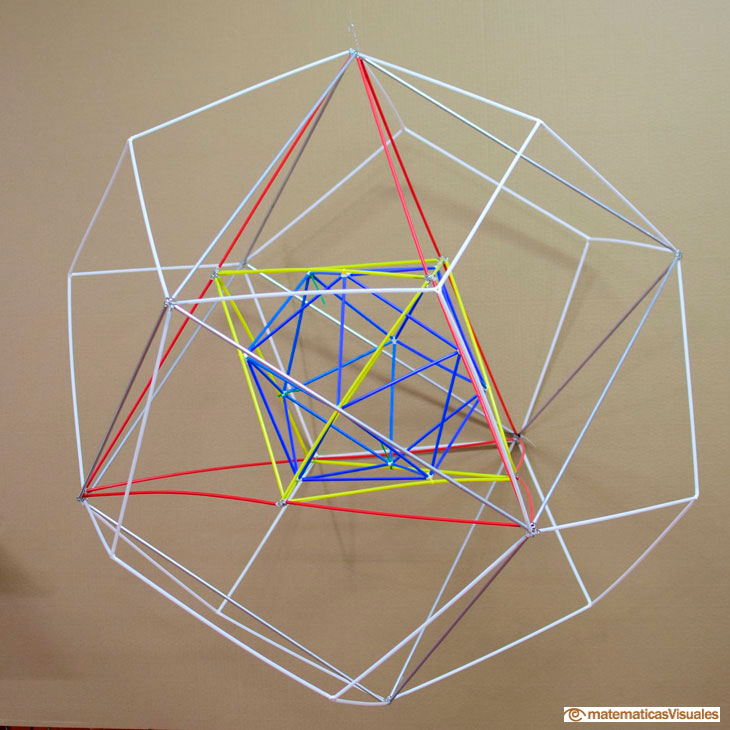
La mediana es la que propuso y construyó Pedro Puig Adam. Él le dió el nombre de 'Omnipoliedro'.

Debido a la relativa complejidad de la figura, las fotos no hacen justicia a su belleza. Por eso se recomienda su construcción y manipulación.

1) El objetivo más importante de este trabajo es animar a profesores, alumnos y personas interesadas a construir esta estructura. Su belleza es suficiente justificación para la actividad. Por eso nos detendremos en hacer una propuesta detallada de la técnica de construcción para mostrar que es mucho más sencilla de hacer de lo que parece. Los materiales de los que disponemos en la actualidad nos facilitan mucho esta agradable tarea. Insistimos en la conveniencia de manipular objetos reales para comprenderlos mejor.

2) Mostrar que esta actividad no es nueva ni innovadora. En la década de 1959, Pedro Puig Adam la construye en el Instituto San Isidro de Madrid. Se ha realizado en muchas ocasiones más, de las que destacaremos la del Tossal de Alicante y la de Matematicas interactivas y manipulativas. En las Referencias iré añadiendo todas la información que pueda recabar sobre estas construcciones del Omnipoliedro que se han realizado.

3) La belleza de la construcción está unida a la posibilidad de mostrar muchas propiedades matemáticas sencillas de estos poliedros. Se pueden plantear con diferentes niveles de dificultad. Una ocasión magnífica para revisar los elementos fundamentales de los poliedros: vértices, aristas y caras. También veremos cómo estas construcciones nos ayudan a calcular los volúmenes de estos poliedros con procedimientos sencillos e interesantes. Además nos ayudarán a concebir nuevos poliedros.

En esta página vamos a ir combinando sugerencias para una construcción sencilla del 'Omnipoliedro' con la descripción de propiedades matemáticas de estos poliedros.

Por si fuera conveniente, se incluye un enlace con información básica sobre los cinco sólidos platónicos:

Aunque no es necesario para la construcción, en algún momento se hablará de la dualidad entre los sólidos regulares. El siguiente enlace puede ser una introducción básica a ese concepto:

Podemos decir que el núcleo de esta construcción lo forman el octaedro dentro del tetraedro que colocacmos dentro del cubo.

Sin entrar en detalles, que ya veremos luego, esta construcción es muy sencilla y muy interesante desde el punto de vista matemático. A partir de ella podemos obtener varias conclusiones matemáticas en las que intervienen estos tres poliedros.

Veremos que estos tres poliedros están relacionados con la raíz cuadrada de dos y la raíz cuadrada de tres. El icosaedro y el dodecaedro requieren un poco más de habilidad pues está relacionadas con la razón áurea.

No hay duda a la hora de construir el dodecaedro pues se hará sobre el cubo. Este procedimiento de añadir unos tejadillos al cubo para formar el dodecaedro regular era conocido desde la AntigÜedad y también nos lo muestra Kepler.

Para colocar el icosaedro tenemos dos posibilidades que se analizarán:

Podemos colocar el icosaedro sobre el dodecaedro. En este caso, ambos poliedros se entrecruzan. Esta es la propuesta que hizo Pedro Puig Adam y hay buenos motivos que la justifican.

Una segunda posibilidad, muy bonita, es colocar el icosaedro en el interior de la construcción. Se puede construir un icosaedro dentro de un octaedro. Realizar esta construcción es más sencillo de lo que parece en cuanto comprendemos mejor estos dos poliedros.

La exposición se organiza en torno a esta variante. Sin embargo, en esta página, vamos a tratar primero el Omnipoliedro de Puig Adam. Me parece más sencilla de construir. Veremos una propuesta de construcción y las consecuencias matemáticas que podemos obtener de ella.

Después comentaremos la variante. También tiene mucho interés y belleza.

Estas construcciones y, en particular, el Omnipoliedro se han realizado con varillas macizas (por ejemplo, de madera) o con tubos.

Nosotros nos vamos a centrar en los tubos. Esos tubos suelen ser de plástico o aluminio. Para construcciones grandes se han usado tubos de PVC.

Propondremos dos construcciones de tamaño mediano. El material principal será tubitos de plástico de los que se usan para sujetar globos. También podemos usar aluminio.

Una ventaja del plástico es que es de colores, barato y muy fácil de conseguir. Por otra parte, es un producto que no está normalizado y se encuentra con diámetros diferentes. Nos tenemos que adaptar a esa situación.

Si optamos por usar el aluminio en algún poliedro es muy adecuado el que tiene un diámetro de 6 mm.

La longitud de estas varillas de plástico y aluminio va a determinar el tamaño de nuestra construcción (en cualquier de las dos posibilidades).

Uniremos los tubos con tacos y hembrillas. Hay que buscar los tacos que nos vengan bien para insertarlos en nuestros tubos. En mi caso he usado tacos de 5 mm. Tener en cuenta que no todos los tacos de esa medida son iguales. Por ejemplo, una conocida marca de tacos vende dos modelos que tienen un grosor ligeramente diferente. Todo queda mejor si las dos embrillas de cada arista están 'paralelas'.

Para unir las hembrillas usaremos bridas. Pueden ser de colores y lo más pequeñas posible. Usaremos muchas pues en el proceso de construcción probablemente tengamos que cortar alguna para reorganizar los vértices.

Para cortar las varillas y las bridas podemos usar alguna de estas herramientas de corte. Una tijera puede ser inadecuada para cortar las bridas.

Una primera prueba de montaje:

Iremos montando los poliedro sin temor a equivocarnos. Sabemos que en algunos vértices hay aristas de varios poliedros. Al principio eso no importa. Unimos las aristas de un poliedro con bridas que luego serán cortadas y sustituidas por otra brida conforme avancemos en la construcción. Es normal que las hembrillas en los vértices queden desordenadas. Cuando un vértice esté completo, podemos cortar la brida y reorganizar las aristas. Al final, los vértices quedarán ordenadas. Por ejemplo, aquí vemos cómo se unen el octaedro (color plata) con el tetraedro (rojo):

En este vértice se unen el tetraedro (rojo), el cubo (verde) y el dodecaedro (blanco):

Este procedimiento de construir poliedros nos lleva a fijarnos más en las aristas y en los vértices. Construimos el esqueleto del poliedro. Las caras quedan vacías.

Otras maneras habituales de unir tubitos de plástico o metal (en particular, pajitas de refresco) es con limpiapipas (que ahora se pueden comprar en cualquier bazar o tienda de manualidades) y con lana.

Con estas técnicas aprendemos que unos poliedros son rígidos pero que otros no mantiene su forma.

Los poliedros formados por triángulos, como el icosaedro, el tetraedro y el octaedro, tienen la particularidad de que si se construyen uniendo varillas, la estructura resultante es rígida. Este hecho tiene aplicaciones en Arquitectura e Ingeniería. Otro ejemplo de este tipo de estructuras son las cúpulas geodésicas.

Sin embargo, el cubo y el dodecaedro no son rígidos.

En nuestras construcciones, el tetraedro es el que aporta la rigidez al cubo (en realidad es la combinación del tetraedro y el octaedro, como veremos luego). Luego construiremos el dodecaedro sobre el cubo y allí perderemos la rigidez.

Para dar rigidez al dodecaedro emplearemos dos soluciones.

La primera es usar la propuesta de Puig Adam y montar el icosaedro de modo que sus aristas se crucen con las del dodecaedro.

La segunda es hacer doce vértices del dodecaedro con la impresora 3D y de este modo los vértices darán rigidez al dodecaedro.

Se quiere divulgar, una vez más, la construcción del Omnipoliedro en sus dos variantes.

Para aquellos que lo consideren útil iremos concretando las medidas de las aristas de cada uno de los poliedros.

Como luego veremos, la arista más larga es la del tetraedro pero está dividida por la mitad. Entonces la arista más larga es la del cubo, quedando la media arista del tetraedro en segundo lugar.

La longitud de las varillas que vayamos a utilizar y esas consideraciones limitan el tamaño de nuestro Omnipoliedro.

Propuesta 1)

Se trata de realizar el Omnipoliedro de Puig Adam usando varillas de plástico de las que se usan para los globos, tacos, hembrillas y bridas.

Es la más sencilla y los materiales se consiguen muy fácilmente. El tamaño, sin ser muy grande, es espectacular. Cada poliedro se construye de un color diferente. Con todos los materiales preparados se construye en una tarde.

La longitud de la varilla es de 36 cm. aproximadamente. Esta va a ser la longitud de la arista del cubo (que resulta ser la misma que la del icosaedro). El icosaedro dará rigidez al dodecaedro.

Propuesta 2)

Si lo que se desea es construir una figura un poco más grande se pueden usar varillas de alumnio para las aristas del cubo. En este caso, la longitud de las varillas de plástico se corresponden con media arista del tetraedro (que, como antes, coincide con la arista del octaedro).

El tamaño del octaedro nos permitirá colocar en su interior el icosaedro.

Para resolver la falta de rigidez del dodecaedro recurriremos a unos vértices hechos con impresora 3D.

Pedro Puig Adam (1900-1960) construyó un omnipoliedro en el Instituto San Isidro de Madrid.

Publicó información e instrucciones de construcción en alguno de sus libros. Eugenio Roanes Macías, de la Sociedad de Profesores Puig Adam, me indicó que en el libro de Puig Adam 'La Matemática y su enseñanza actual' se mencionaba la construcción del Omnipoliedro. Gracias a Jesús Velázquez, bibliotecario de la Universidad de Zaragoza, he podido consultar el libro.

'La Matemática y su enseñanza actual' fue publicado en 1960. Su capítulo VI se titula 'El material'. Dentro del apartado 'Varillas engarzadas y articuladas', Puig Adam escribe sobre el omnipoliedro (páginas 249-261).

Cuenta Puig Adam que una reflexión sobre la rigidez de los poliedros llevó a que 'los alumnos comprobaron la rigidez del icosaedro como estructura triangular, obtenida como hemos dicho, sin necesidad de soldar los vértices, sino de atarlos simplemente'.

'En cambio, un dodecaedro construido de análoga manera carece de rigidez. Para dársela hubo que sostenerle mediante un icosaedro formado por aristas que cruzaran ortogonalmente las del dodecaedro en sus puntos medios. Es fácil obtener la relación entre las aristas de uno y otro poliedro: la arista del dodecaedro es la sección áurea de la del icosaedro cruzado'.

Entonces se coloca un cubo dentro del dodecaedro, un tetraedro dentro del cubo y un octaedro dentro del tetraedro.

'Este modelo fue bautizado con el nombre de "omnipoliedro regular" por los propios alumnos que lo construyeron, en el Instituto de San Isidro'.

Concluye Puig Adam: 'Quede consignado lo anterior como un ejemplo vivido de cómo el material multivalente de varillas permite la rápida construcción de un modelo, y cómo esta construcción puede surgir del comentario de un hecho ocasional de la misma vida escolar'.

Descarga del capítulo VI del libro de Puig Adam 'La Matemática y su enseñanza actual' dedicado al material didáctico matemático. Incluye un apartado dedicado al juguete y otro a las películas matemáticas.

Leer a Puig Adam sigue siendo actual después de más de sesenta años. Hay que tener en cuenta que Puig Adam compartió experiencias con Emma Castelnuovo, Fletcher, Gattegno y otros muchos. Como otro reflejo de esa época, se puede ver una breve referencia a dos trabajos de Gattegno y Nicolet en matemáticasVisuales.

Obtener más información sobre el trabajo de Puig Adam sobre el omnipoliedro sería muy interesante: escaneado de las páginas de sus libros en las que escribió sobre esta construcción, información sobre la construcción en el Instituto San Isidro, registro fotográfico de ese trabajo...

Se agradecerá cualquier aportación sobre este tema.

Empezamos el comentario sobre la construcción con el octaedro.

La construcción del octaedro con tubitos nos muestra la rigidez del poliedro.

Por otra parte, al manipular esta construcción nos damos cuenta de una propiedad que quizás ha pasado inadvertida si consideramos un octaedro macizo o hecho con cartulina.

Esta propiedad es que los seis vértices del octaedro se encuentran en los vértices de tres cuadrados ortogonales dos a dos.

Esto todavía se ve más claro si construimos el octaedro con origami de este modo:

Si el octaedro va a ser el primer poliedro de nuestro Omnipoliedro, ¿qué longitud de las varillas podemos utilizar?

Conforme avance la construcción veremos que la relación entre las aristas del octaedro (A_O) y las del cubo (A_C) es:

Un caso concreto: las varillas miden 36 cm. Si añadimos las dos hembrillas, las aristas del cubo miden 38 cm.

Por lo tanto, las varillas del octaedro, con hembrillas, medirán 26,9 cm. aproximadamente. Es decir, necesito cortar 12 varillas de 24,9 cm.

Construimos el tetraedro sobre el octaedro.

Lo hacemos añadiendo cuatro tetraedros sobre cuatro caras el octaedro.

Por lo tanto, la arista del tetraedro (A_T) es el doble que la del octaedro (A_O).

En nuestrar construcción necesitamos 12 medias aristas del tetraedro que tienen la misma medida que las del octaedro.

Aunque sea desviarnos de nuestra construcción, este es un momento adecuado para plantearnos qué ocurre si añadimos otros cuatro tetraedros en las caras del octaedro que han quedado libres.

Lo que obtenemos es un poliedro muy bonito y que se conoce desde tiempo inmemorial. Fue dibujado por Leonardo da Vinci. Kepler lo llamó 'Stella octangula', es decir, estrella de ocho puntas.

Si partimos del octaedro y prolongamos sus caras hasta que se vuelvan a cortar obtenemos la 'Stella octangula'. Por este motivo, el poliedro es un octaedro estrellado.

El tetraedro es dual de si mismo o autodual. También decimos que es dual de otro tetraedro. Estamos colocando dos tetraedros de modo que sus aristas se bisequen ortogonalmente. Estos dos tetraedros (duales) están en 'posición recíproca'. Su intersección es el octaedro.

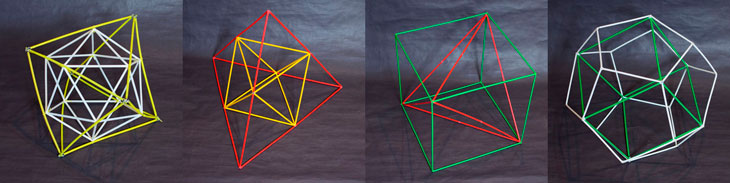
En la siguiente construcción podemos ver dos tetraedros (verde y rojo) en posición recíproca, su intersección es un octaedro (amarillo) y, dentro del octaedro, un cubo realizado en cartulina verde. La colocación del cubo y del octaedro muestra su dualidad de un modo típico.

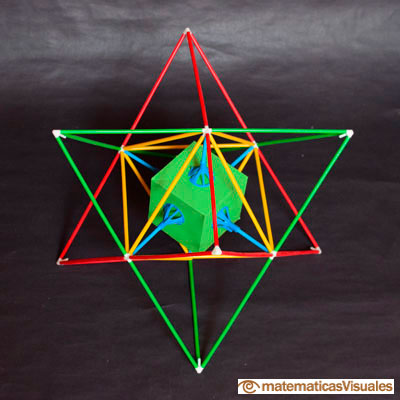
Al construir la Stella Octangula todavía queda más clara la relación entre el cubo y el tetraedro pues los ocho vértices de la Stella Octangula están en los vértices de un cubo. Esta relación la estudiamos en la siguiente sección.

Construimos el cubo sobre el tetraedro.

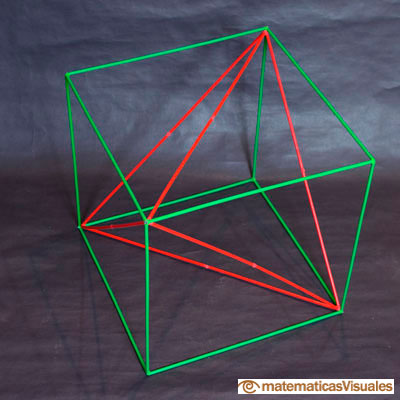
Las seis aristas del tetraedro son diagonales de las seis caras del cubo.

El tetraedro da rigidez al cubo.

Por esta construcción, y aplicando el teorema de Pitágoras, podemos comprender la relación entre las aristas del tetraedro (A_T) y las del cubo (A_C):

Tenemos en cuenta que en nuestro Omnipoliedro, las aristas del tetraedro están cortadas por la mitad.

La construcción que tenemos hasta ahora es muy bonita: dentro del cubo está el tetraedro y dentro del tetraedro, el octaedro.

Si nos fijamos en los seis vértices del octaedro vemos que están en el centro de las caras del cubo. El cubo y el octaedro intercambian el número de vértices y de caras. Tienen el mismo número de aristas. Son poliedros duales.

Por otro lado, como hemos comentado, dentro del cubo podríamos poner dos tetraedros (en posición recíproca, formando una 'Stella octangula'). La envoltura de la 'Stella octangula' es el cubo y la intersección de los dos tetraedros es el octaedro.

Kepler considera al cubo uno de sus tres poliedros rómbicos. Las caras del cubo son rombos (rombos rectángulos, es decir, cuadrados). Kepler descubrió dos poliedro rómbicos, el dodecaedro rómbico y el triacontaedro.

Podemos suponer cómo Kepler descubre los tres poliedros rómbicos. Es solo una suposición pues no sabemos cómo lo hizo.

Vamos a verlo con dos tetraedros. Partimos de una pareja de poliedros duales, en nuestro caso, los dos tetraedros. Los colocamos en 'posición recíproca'. Su intersección es un poliedro (el octaedro) y su envoltura es un poliedro rómbico (el cubo). Ambos poliedros son poliedros duales.

Más adelante repetiremos esta idea para encontrar el triacontaedro.

Construimos el dodecaedro sobre el cubo.

Esta construcción, que ya era conocida en la Antigüedad, fue dibujada por Kepler. Consiste en añadir unos tejados al cubo.

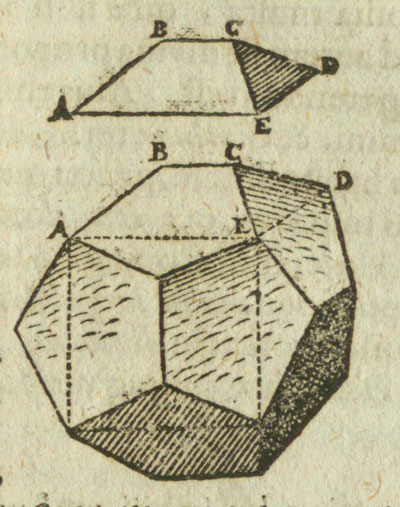
Nos fijamos que una arista del cubo es una diagonal del pentágono. Por lo tanto, la longitud de la arista del cubo y la del dodecaedro están relacionadas por la proporción áurea.

Por lo tanto, la arista del dodecaedro (A_D) será:

Hemos visto que cada arista del cubo es una de las diagonales de un pentágono. Pero el pentágono tiene cinco diagonales y podemos colocar cinco cubos dentro de un dodecaedro.

Este precioso recortable todavía se puede comprar (después de muchos años). Lo publicó la editorial Tarquin (Advanced Polyhedra 3: The Compound of Five Cubes).

Dentro de cada cubo podemos poner un tetraedro. Luego podemos colocar cinco tetraedros dentro de un dodecaedro. Aquí tenemos un ejemplo hecho con la técnica de origami modular.

En realidad podemos colocar dos tetraedros en cada cubo (formando una 'Stella octangula'). Es decir, dentro del dodecaedro podemos poner diez tetraedros.

Después de este paseo por alguna de las propiedades del dodecaedro y su relación con otros poliedros, volvamos a nuestra construcción del Omnipoliedro.

Lo que apreciamos es que el dodecaedro construido sobre el cubo no tiene rigidez. La rigidez se la va a dar el icosaedro.

Lo que hice fue construir el dodecaedro y el icosaedro al mismo tiempo como se muestra en la siguiente fotografía:

En la construcción del Omnipoliedro que estamos haciendo (que es la propuesta por Puig Adam) el icosaedro y el dodecaedro no están uno dentro del otro. Se entrecruzan.

El siguiente modelo, con ambos poliedros, está realizado con Zome:

Notamos que ambos poliedros son duales. Sus aristas se bisecan y son ortogonales. Es decir, el icosaedro y el dodecaedro están en 'posición recíproca'. Ya hemos visto anteriormente dos tetraedros en 'posición recíproca'. Más adelante profundizaremos un poco en esta idea.

Desde el punto de vista de la construcción nos interesa saber la longitud de la arista del icosaedro (A_I). Resulta que es la misma que la del cubo. Esto lo deduciremos más adelante.

Con esta información ya podemos completar nuestro Omnipoliedro.

Este va a ser nuestro resultado. La fotografía de esta construcción no hace justicia con el modelo real. En él se aprecian claramente los cinco poliedros y es muy bonito.

En esta propuesta de construcción del Omnipoliedro buscamos la simplicidad. Que los materiales sean fáciles de conseguir y que su montaje sea sencillo.

La manera más simple de construir dos poliedros en 'posición recíproca' es colocar las aristas del segundo poliedro 'por encima' o 'por debajo' y unirlas con una brida.

En mi caso he optado por cortar la aristas del icosaedro con su longitud teórica (igual a la del cubo) y montar las aristas del icosaedro 'por debajo' de las del dodecaedro. Ya sabía que habría que ajustar estas aristas pues no iban a quedar rectas.

Una vez montado decidí recortar las aristas 1 cm. aproximadamente.

Fui marcando con cinta de carrocero las aristas que iba cortando.

La misma técnica se puede usar al final de la construcción para revisar que las aristas del icosaedro y las del dodecaedro se bisecan. Cada unión revisada se puede marcan de la misma manera.

Todos estos detalles se comentar por si a alguna persona le resultan de utilidad.

La construcción es muy sencilla y los posibles errores se corrigen con facilidad.

Hay maneras más elegantes de construir poliedros en 'posición recíproca'. Se pueden cortar las aristas por la mitad y unirlas con cruces de plástico. Estas cruces pueden estar hechas con impresora 3d.

También se pueden usar unas cruces que usan los albañiles para colocar baldosas (y dejar un hueco igual entre ellas). Estas cruces se venden en las tiendas de materiales de construcción, pueden ser de varios tamaños y son baratas.

Ya hemos podido construir el omnipoliedro según la propuesta de Puig Adam. Pero nos falta calcular la arista del icosaedro.

El icosaedro y su dual, el dodecaedro, son dos poliedros de particular belleza. Ambos están relacionados con la proporción áurea y su estudio es un poco más complicado que el de los otros tres sólidos platónicos.

Sin embargo, si tenemos modelos de estas construcciones, los razonammientos que se hacen sobre estos poliedros se vuelven muy claros. Son ejemplos excelentes de cómo la construcción de poliedros nos ayuda a pensar y a comprender propiedades matemáticas.

Lo que queremos justificar es que la longitud de la arista del icosaedro (A_I) es la misma que la del cubo (A_C). Es decir:

Para empezar necesitaremos estudiar el icosaedro.

Si nos fijamos en nuestra construcción del dodecaedro y del icosaedro veremos que sus aristas se cortan. El punto de intersección de cada par de aristas es el punto medio de ambas. Cada par de aristas se cortan ortogonalmente.

En nuestra construcción vemos que el dodecaedro y el icosaedro comparten la misma interesfera. Este es el punto clave del razonamiento.

Vamos a calcular los radios de las interesferas del icosaedro y del dodecaedro.

Un repaso a la siguiente página sobre el icosaedro nos puede ayudar a calcular el radio de la interesfera de un icosaedro (por ejemplo, de arista 2):

Las flechas señalan radios de la interesfera:

Como sabemos, la relación del icosaedro con la razón áurea es fundamental.

Por lo tanto, el radio de la interesfera (o esfera media) del icosaedro de arista 2 (M_I(2)) es:

El estudio del dodecaedro es un poco más difícil. La siguiente página nos puede ayudar:

Aquí está representado un radio de la interesfera del dodecaedro.

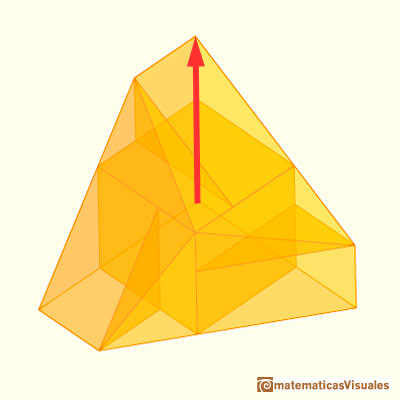
Esta es su medida para un dodecaedro de arista 2 (M_D(2)):

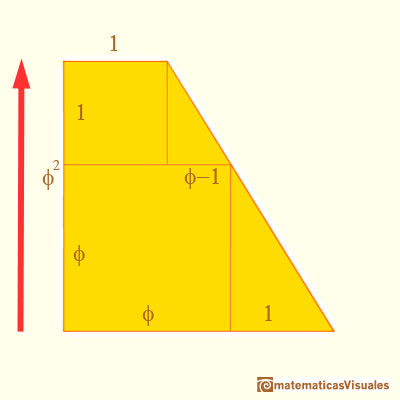
Por lo tanto, si queremos que ambos poliedros tengan la misma interesfera debemos multiplicar la arista del dodecaedro para obtener la arista del icosaedro.

Recordamos la relación entre la arista del dodecaedro y la del cubo:

Por lo tanto, obtenemos la relación entre la arista del icosaedro y la del cubo que andábamos buscando:

Esto es un ejemplo de cómo la construcción de modelos nos ayuda a hacer cálculos que, de otra manera, quizás serían complicados.

Al construir el dodecaedro y el icosaedro nuestra construcción del Omnipoliedro, según la propuesta de Puig Adam, ha terminado.

Para aquellos lectores interesados vamos a profundizar un poco más.

La relación entre ambos poliedros, tal como están colocados, es muy interesante y vamos a comentar cómo esta figura nos abre el horizonte hacia otros poliedros.

El dodecaedro y el icosaedro forman una pareja de poliedros duales. Tal como están colocados ambos poliedros se entrecruzan. Están en 'posición recíproca'.

La reflexión que vamos a hacer es análoga a la comentada para el caso de los dos tetraedros formando la 'Stella octangula'. Recordamos que entonces su intersección era el octaedro y su envoltura el cubo. En este caso, los tres poliedros implicados son poliedros regulares.

En nuestro caso, resulta que la intersección entre el dodecaedro y el icosaedro es un poliedro que tiene pentágonos y triángulos. Pertenece a la familia de los poliedros arquimedianos y se llama icosidodecaedro.

La figura formada por el icosaedro y el dodecaedro es un icosidodecaedro estrellado. Se obtiene al prolongar las caras del icosidodecaedro hasta que se vuelven a cortar.

Las aristas del dodecaedro y del icosaedro se bisecan y los vértices forman treinta rombos (las diagonales están en proporción áurea).

Este poliedro rómbico fue descubierto por Kepler y se llama triacontaedro.

El icosidodecaedro y el triacontaedro son poliedros duales. Debido a que el triacontaedro es dual de un sólido arquimediano resulta que el triacontaedro es uno de los sólidos de Catalan.

En la siguiente fotografía fue tomada en la exposición 'Kepler, las abejas y el dodecaedro rómbico'. Vemos en la parte superior tres figuras. La de la izquierda y la central representan otras dos maneras habituales de representar la dualidad entre dodecaedro e icosaedro. La de la derecha es un icosidodecaedro (cartulina, violeta) dentro de un triacontaedro (Zome, rojo) mostrando también la dualidad entre estos dos poliedros.

La figura más grande está formada por un dodecaedro (blanco), un icosaedro (azul), su intersección, el icosidodecaedro (amarillo) y su envoltura, el triacontaedro(rojo):

Kepler descubrió otro poliedro rómbico: el dodecaedro rómbico. Se puede obtener por el mismo procedimiento pero considerando como pareja de sólidos duales al cubo y al octaedro.

Hemos visto que la construcción del Omnipoliedro propuesto por Puig Adam es muy bonita y de ella se puede obtener interesantes resultados matemáticos.

Hay una segunda manera de organizar los cinco sólidos platónicos. Se diferencian en la posición del icosaedro.

Ahora el icosaedro se va a colocar en el interior del octaedro. Es una manera de hacerlo que nos va a enseñar propiedades de ambos poliedros.

Los seis vértices del octaedro están en tres cuadrados ortogonales dos a dos. Los doce vértices del icosaedro están en tres rectángulos áureos que también son ortogonales dos a dos. Esto explica cómo se puede colocar un icosaedro en un octaedro (de hecho, de dos maneras simétricas).

Quizás lo que haga bonita esta construcción es que todos los poliedros están unos dentro de otros. También me gusta que sea el dodecaedro el que rodee a todos los demás. El dodecaedro es el representante del Cosmos o el Universo.

Un inconveniente es que el dodecaedro no es rígido. Para resolver esto he utilizado unos vértices hechos con impresora 3d.

Este es el resultado:

Para hacer la construcción un poco más grande he utilizado tubo de aluminio de 6 mm de diámetro para las aristas del cubo. Si el resto de los poliedros se construyen con varillas de globos, la longitud de la arista del cubo está ahora determinada por la longitud de la arista del octaedro (mitad de la del tetraedro).

Por ejemplo, si la varilla de plástico mide 36 cm. entonces, con las hembrillas, la arista del octaedro medirá 38 cm.

Por lo tanto, la arista del cubo puede medir 53,7 cm.

Y debemos cortar las varillas de aluminio 2 cm más cortas.

Como un complemento vamos a revisar algunos materiales para construir estos poliedros.

La técnica de construcción con cartulina y gomas es muy interesante. También es un material excelente para explorar los poliedros arquimedianos.

Los desarrollos del tetraedro, octaedro e icosaedro son muy sencillos de dibujar al ser sus caras triángulos equiláteros.

El desarrollo del tetraedro es muy fácil de dibujar. También se puede descargar esta plantilla y construirlo.

El desarrollo del octaedro también es muy sencillo de dibujar. También se puede descargar esta plantilla y construirlo.

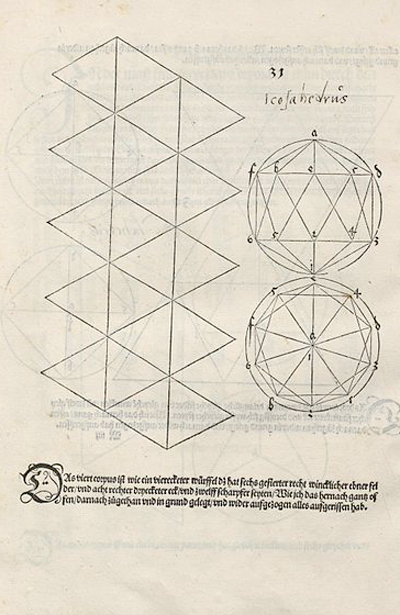
Este es el desarrollo del icosaedro tal como nos enseñó Durero:

El icosaedro se puede construir con este material diseñado por Bruno Munari:

También pegando discos:

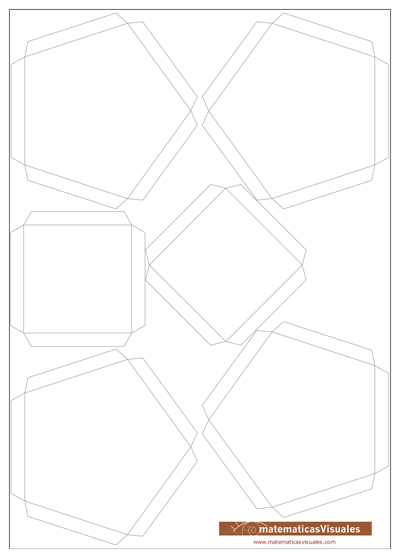
Dibujar el desarrollo del dodecaedro con regla y compás es un reto muy bonito.

Otro procedimiento muy recomendable es recortar las caras independientemente y pegarlas. Así se pueden usar cartulinas de distintos colores. Se pueden usar seis colores de modo que parejas de caras opuestas tengan el mismo color.