Hay una relación muy interesante entre el octaedro y el icosaedro que ya sabemos que son dos sólidos platónicos.
En matemáticasVisuales ya hemos visto el octaedro, cómo se calcula su volumen y su relación con el tetraedro. También sabemos que el cubo y el octaedro son poliedros duales.
Algunas de estas propiedades pueden verse en el siguiente enlace:

También hay varias páginas dedicadas al icosaedro. Un resumen de sus propiedades puede verse en este enlace:

En esta página veremos una construcción muy bonita que relaciona el icosaedro y el octaedro.
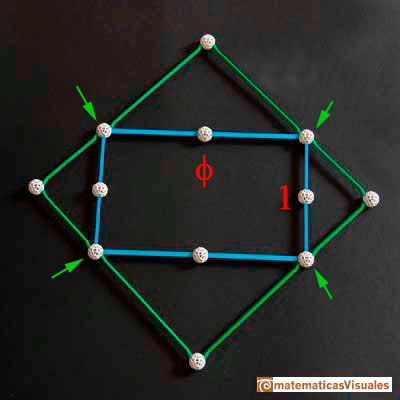
Un octaedro tiene 12 aristas y un icosaedro tiene 12 vértices. Podemos poner un icosaedro dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. De hecho puede hacerse de dos maneras 'simétricas'.
Esta es la construcción hecha con los vértices hechos con impresora 3d. Las aristas son varillas de plástico.

Parece complicado pero es muy simple si nos ayudamos de dos construcciones: una del octaedro y otra del icosaedro.
Además, a partir de esta relación entre estos dos poliedros vamos a poder calcular el volumen del icosaedro.
Y este es el sentido de esta página: cómo las construcciones matemáticas, además de ser bonitas, nos ayudan a comprender conceptos y obtener resultados matemáticos.
La siguiente construcción de origami nos muestra los vértices y aristas de un octaedro y podemos ver su interior.

Esta construcción es muy sencilla y se describe en el siguiente enlace:
Lo que nos interesas destacar ahora para nuestra tarea de inscribir un icosaedro en un octaedro es que vemos que los 6 vértices del octaedro están en tres cuadrados que son ortogonales dos a dos.
Las construcciones del octaedro en las que podemos ver el interior nos ayudan a calcular el volumen del octaedro. Tal como se explica en la siguiente página:

Revisaremos la fórmula del volumen del octaedro más adelante. A partir de ella calcularemos, de un modo sencillo, el volumen de un icosaedro.
Por otra parte, hemos visto otra construcción muy bonita de un icosaedro formado por tres rectángulos áureos que también son ortogonales dos a dos.

Destacamos que tanto en el caso del octaedro como en el del icosaedro sus vértices respectivos están en tres planos que son ortogonales dos a dos. En el caso de octaedro en tres cuadrados y en el del icosaedro en tres rectángulos áureos.
Está construcción la podemos hacer con madera, cartón pluma o cartulina, tal como se explica en el siguiente enlace:
Al igual que con la construcción del octaedro podemos ver el interior del icosaedro y esto nos ayuda a calcular su volumen.

A partir de la construcción que proponermos en esta página veremos otra manera distinta de calcular el volumen del icosaedro.
Ahora vamos a combinar un cuadrado y un rectángulo áureo.
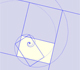
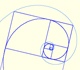
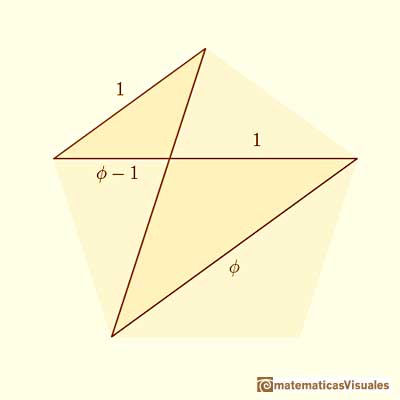
Podemos inscribir un rectángulo áureo en un cuadrado como se muestra en la figura (hecha con Zome):

Vamos a detenernos un poco en esta configuración.
En primer lugar, notamos que los vértices del rectágulo dividen a los lados del cuadrado en la proporción áurea.
En segundo lugar, un segmento se puede dividir en proporción áurea de dos modos distintos. Podemos inscribir un rectángulo áureo en un cuadrado de dos maneras distintas. En un lenguaje de andar por casa diríamos que en la figura anterior el rectángulo está horizontal pero también podría estar vertical.
Este hecho tan simple tendrá como consecuencia que en un octaedro podremos inscribir dos icosaedros de modo que los vértices del icosaedro dividan a los lados del octaedro en la proporción áurea.
Se basa en que los vértices de un icosaedro están en tres rectángulos que son perpendiculares dos a dos y que los vértices de un octaedro están en tres cuadrados que también son perpendiculares dos a dos.
Si colocamos tres cuadrados sobre los que tenemos marcado un rectángulo áureo adecuadamente obtenemos la colocación de los vértices del octaedro y del icosaedro.

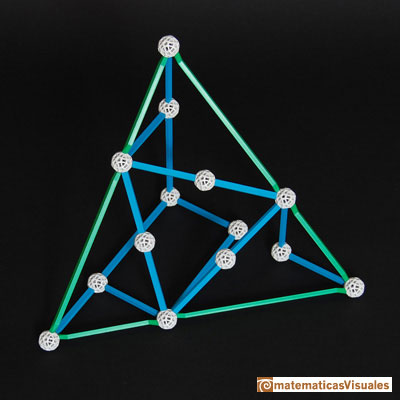
Las figuras en blanco son el esqueleto de las seis bipirámides que tenemos que quitar al octaedro para tener el icosaedro.

Estas bipirámides nos van a ser útiles para calcular el volumen del icosaedro más adelante.

Una solución sencilla para unir los vértices del icosaedro a las aristas del octaedro:

En esta construcción los vértices unen las aristas del icosaedro y del octaedro:


Detalle de los vértices:
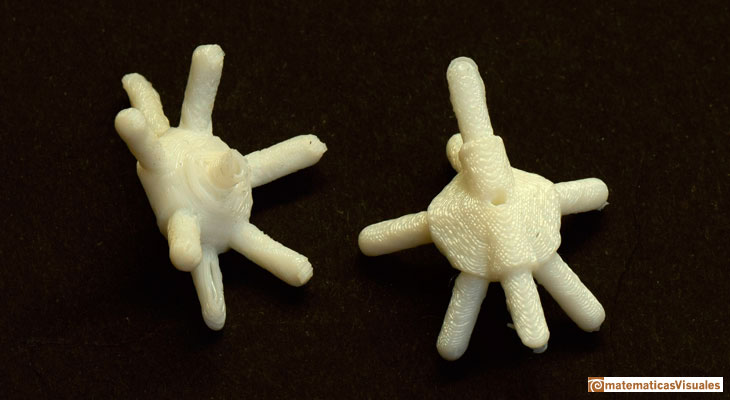

Con un dodecaedro en su interior. El dodecaedro y el icosaedro son poliedros duales.

Esta construcción se puede hacer con Zome:



La cartulina es un material barato y con ella podemos hacer esta construcción.
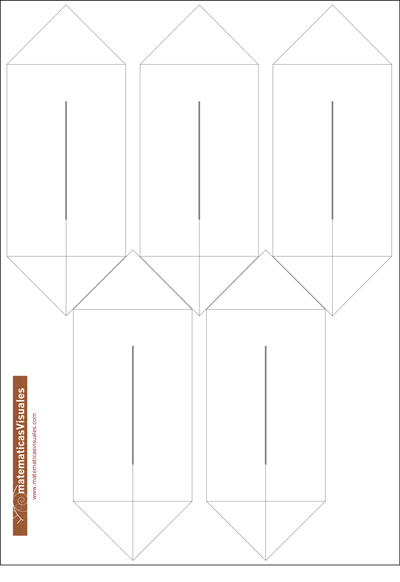
Las siguientes plantillas se pueden descargar y construir los rectángulos áureos 'extendidos' y octavos de octaedro:
Usamos imanes para que las diferentes partes se mantengan unidas.
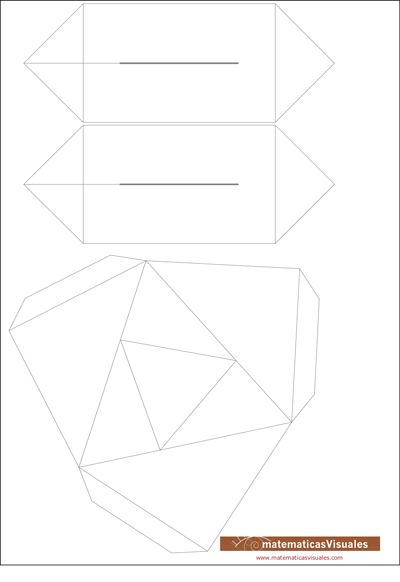
Se pueden combinar con los octavos de icosaedro que podemos descargar en este enlace:

Se obtiene una idea muy clara de la relación entre el octaedro y el icosaedro.





Esta construcción del icosaedro dentro de un octaedro, que hemos hecho con diferentes técnicas, además de ser muy bonita nos va a permitir hacer un cálculo sencillo del volumen del icosaedro.
Aparentemente, calcular el volumen de un icosaedro parece tarea complicada pero no lo es si nos ayudamos de la visión que nos proporcionan las construcciones.
El número áureo juega un papel importante en este asunto. Para simplificar los cálculos nos vendrá bien repasar alguna propiedad del número áureo.
Ya hemos visto el número áureo, su relación con la diagonal de un pentágono regular y algunas propiedades del rectángulo aúreo en enlaces como los siguientes:


Ya sabemos la ecuación que cumple el número aúreo:
Podemos escribir la segunda potencia de phi como suma de la potencia 0 y la potencia 1:
Si vamos multiplicando por phi cada fila podemos comprobar que se cumple que cada potencia es la suma de las dos potencias anteriores.
Este último resultado lo usaremos más adelante.
Podríamos continuar todo lo que quisiéramos. Esta relación entre las sucesivas potencias de phi, que llamamos de recurrencia, es análoga a la de la sucesión de Finobacci.
Queremos calcular el volumen del icosaedro que tiene arista 1. Para ello calcularemos el volumen del octaedro que lo contiene.
Repasamos el volumen del octaedro:

El volumen del octaedro de arista 1 es:
Entonces, El volumen del octaedro de arista a es:
Para calcular el volumen del octaedro que nos interesa tenemos que calcular el lado del cuadrado a partiendo de que el ancho del rectángulo mide 1.
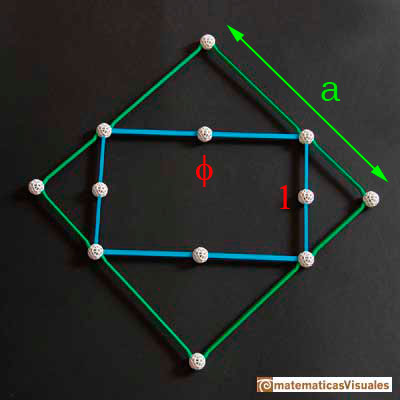
El volumen del octaedro que contiene al icosaedro es:
Podemos simplificar la expresión:
Si queremos calcular el volumen del icosaedro de arista 1 tendremos que restar al volumen del octaedro el volumen de seis bipirámides.
Con la notación que estamos utilizando, esta expresión la podemos escribir así:
Este es es esqueleto de una de estas bipirámides

Estas bipirámides están formadas por dos pirámides cuyas bases son un triángulo equilátero rectángulo.
El área A es fácil de calcular.

El volumen de una bipirámide será un tercio del área de la base por la altura. Nos fijamos en lo que mide la altura y calculamos el volumen de una bipirámide:

Por lo tanto, el volumen de un icosaedro de arista 1 lo podemos escribir:
Simplificando, resulta:
De este modo, una construcción bonita nos ha ayudado a calcular el volumen de un icosaedro.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES