Sesión del Taller de Talento Matemático de Zaragoza por Roberto Cardil.
Viernes 13 de Abril de 2012 a las 18:15.
Objetivos:
El primer objetivo es pasar un rato agradable compartiendo técnicas que hayamos usado para construir poliedros con diferentes materiales.
Estas construcciones nos proporcionan un placer estético y nos ayudan a desarrollar nuestra visión espacial. Un segundo objetivo es mostrar que también nos pueden ayudar a obtener resultados matemáticos.
En esta sesión nos centraremos en los sólidos platónicos, en particular en los más sencillos: cubo, tetraedro y octaedro. Repasaremos los volúmenes de estos poliedros y veremos cómo su construcción nos facilita la tarea. Veremos algunas construcciones del icosaedro y del dodecaedro.
Aprenderemos a construir un tetraedro con origami modular.
Un guión de lo que podemos ver es el siguiente:
La primera vez que me encontré con un tetraedro por la calle fue cuando la gaseosería que había enfrente de mi casa empezó a vender horchata en un nuevo envase de papel parecido al de la siguiente figura. Este invento lo había hecho Erik Wallenberg, un ingeniero sueco y lo había desarrollado la empresa TetraPack. Viendo las imágenes te puedes imaginar como se fabricaba.
PARA PENSAR UN POCO
Estos envases tetraédricos tenían muchas ventajas (¿Te imaginas cuáles?), sin embargo, actualmente prácticamente no se utilizan. ¿Qué inconvenientes tienen los envases tetraédricos?
Los envases de horchata y de leche contenían medio litro. Nos interesa calcular las dimensiones del tetraedro y su volumen.
El tetraedro es una pirámide y su volumen es un tercio del área de la base por la altura. Así podemos calcular su volumen pero vamos a ver una construcción (que ya nos enseñó Kepler) que nos va a facilitar la tarea.
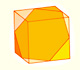
Se puede construir un tetraedro dentro de un cubo:
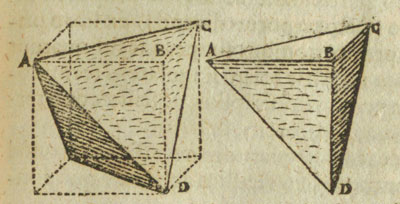
Los desarrollos del tetraedro y del cubo son los más sencillos de dibujar. Si el cubo tiene 10 cm. de arista, ¿cuál es la arista del tetraedro?

PARA PENSAR UN POCO
A partir de esta construcción podemos calcular el volumen de un tetraedro de arista 1:

|
Volumen del tetraedro
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
|
Hagamos un tetraedro con tubos. La estructura es rígida.
PARA PENSAR UN POCO
Si hacemos un tetraedro con tubos pero cada arista es de dos tubos de largo. ¿Qué relación tienen los volúmenes de estos dos tetraedros?
Volveremos a esta construcción más adelante.
Una técnica con muchas posibilidades es el origami modular. Construiremos este tetraedro con dos unidades o módulos:
PARA PENSAR UN POCO
Los dos primeros dobleces se muestran en la siguiente imagen. ¿Podemos justificar que el doblez es medio triángulo equilátero?
Estos son los pasos para construir el tetraedro. Los pendientes son un regalo de la profesora Inmaculada Ordóñez Ríos que colabora en el sitio web Matematicas Interactivas y Manipulativas y que fue quién me enseñó esta figura.

Si nos fijamos en los cuatro vértices podemos hacer una construcción de este tipo:
En resumen, el tetraedro es el poliedro platónico que tiene 4 vértices, 6 aristas y cuatro caras que son triángulos equiláteros.
Podemos pensar que el octaedro está formado por dos pirámides de base cuadrada unidas. Su desarrollo es fácil de construir pues sus caras son triángulos equiláteros.
Si nos fijamos en los seis vértices podemos hacer una construcción de este tipo:
Una figura de origami modular sencilla e instructiva está formada por los tres cuadrados en planos ortogonales dos a dos que contienen las 12 aristas y los 6 vértices del octaedro regular.
PARA PENSAR UN POCO
A partir de esta construcción podemos calcular el volumen de un octaedro:

|
Volúmenes del octaedro y del tetraedro
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
|
Ya sabemos calcular el volumen de un octaedro y el de un tetraedro. Hay una relación sencilla entre estos dos volúmenes que esta construcción nos ayuda a entender:
El icosaedro tiene veinte triángulos equiláteros. Su desarrollo, por tanto, es sencillo de construir.
Con gomas: lámpara icosaedro

La siguiente construcción es muy bonita e interesante. Los vértices de un icosaedro están en tres rectángulos áureos que están en tres planos ortogonales dos a dos.
Esta construcción está hecha con madera pero se puede hacer con cartón o cartón pluma. En cada vértice hay un alfiler y las aristas son hilo con goma.

PARA PENSAR UN POCO
Está claro, por la construcción de la figura, que algunos triángulos son equiláteros. ¿Lo son todos? ¿Cómo lo podemos justificar?
Los tres planos que contienen los vértices del icosaedro están enlazados formando los Anillos de Borromeo.
Esta construcción con globos muestra los anillos de Borromeo. Inspirada en el vídeo del logotipo de la International Mathematical Union (IMU) que fue diseñado por John Sullivan (The Borromean Rings: a new logo for the IMU)
El octaedro también tiene los vértices en tres planos paralelos. Podemos usar esta propiedad común para construir un icosaedro dentro de un octaedro con tubos.
El icosaedro también inspira una construcción sencilla de tensegridad.

Desarrollo del dodecaedro
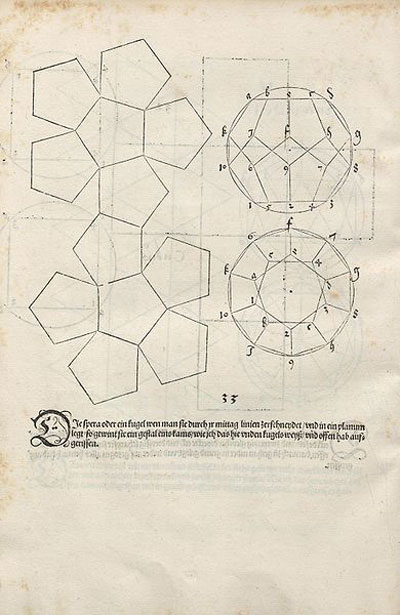
¡Disfrutad construyendo poliedros!
 SIGUIENTE
SIGUIENTE

MÁS ENLACES