Construcción de poliedros. Técnicas sencillas
La cartulina de colores es un material muy indicado para construir poliedros. La primera técnica consiste en dibujar el desarrollo plano del poliedro,
recortarlo y pegarlo.
Algunos trucos cuando trabajamos con cartulina son: para marcar bien las aristas conviene usar una tijera abierta y una regla. Usar un pegamento transparente.
Cuando nos quede alguna arista mal pegada podemos usar un triangulo de cartulina con pegamento para poner pegamento dentro de la arista. Algunas veces, la
última solapa se resiste y hay que usar un alfiler para ponerla en su sitio.
Los desarrollos del tetraedro y del cubo son los más sencillos de dibujar. Si el cubo tiene 10 cm. de arista, ¿cuál es
la arista del tetraedro?
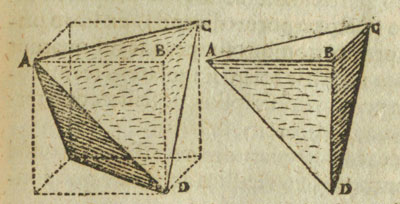
Esta construcción ya fue dibujada por Kepler y nos va a ayudar a calcular el volumen de un tetraedro
de un modo sencillo:
La primera vez que me encontré con un tetraedro por la calle fue cuando la gaseosería que había enfrente de mi casa
empezó a vender horchata en un nuevo envase de papel parecido al de la siguiente figura. Este invento lo había hecho
Erik Wallenberg, un ingeniero sueco y lo había desarrollado la empresa TetraPack. Viendo las imágenes te puedes
imaginar como se fabricaba.
Se puede cortar un cubo por la mitad de modo que la sección sea un hexágono regular.
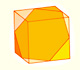
Podemos cortar un cubo por la mitad con un plano de modo que la sección sea un hexágono regular. Ocho de estos medios cubos forman un octaedro truncado.
Desarrollo del medio cubo para descargar, imprimir, recortar y montar
Ocho de estos medios cubos pueden formar un octaedro truncado, un poliedro que tesela el espacio (al igual que el cubo)

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
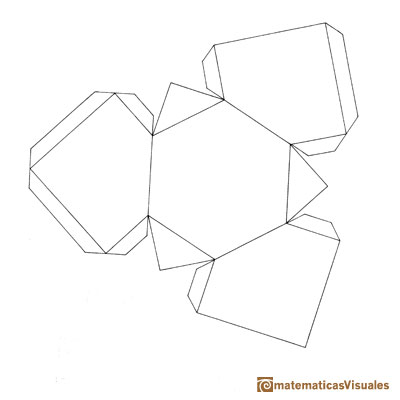
Construir un dodecaedro dibujando su desarrollo es una actividad muy recomendable y satisfactoria pues es un poliedro
muy bonito y que es más difícil de dibujar que el resto de los sólidos platónicos (formados por cuadrados y triángulos
equiláteros).
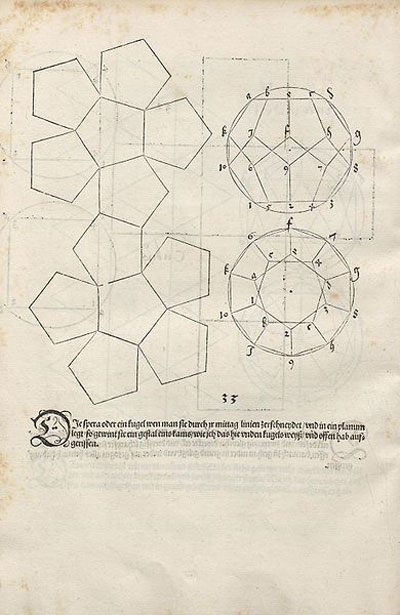
Este es el desarrollo del dodecaedro según Durero:
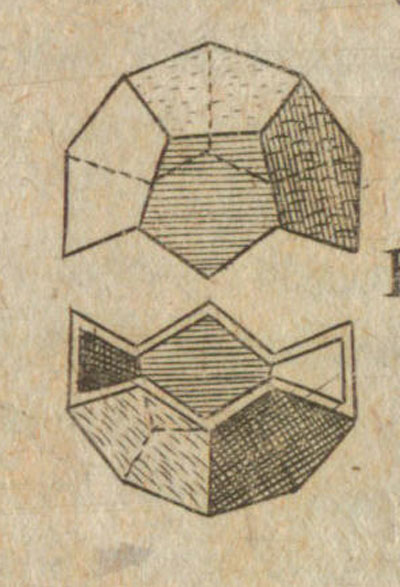
Kepler también se interesó por el dodecaedro:
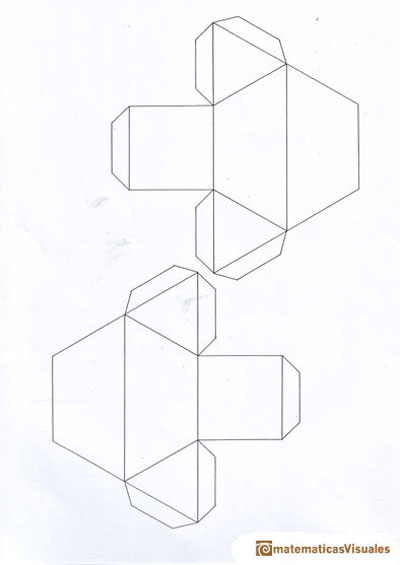
Con esas dos piezas se tiene que construir un tetraedro.
Quizás no lo parezca a primera vista, pero cada pieza esta formada por dos tetraedros y medio octaedro. Volveremos a
esta idea más adelante.
REFERENCIAS
George Hart es una referencia para todos los aficionados a la construcción
de poliedros.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. Una traducción española fue hecha por Luis Bou García y fue publicada por la Editorial
Salvat con el título 'Instantáneas Matemáticas' en 1986.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.

Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
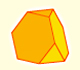
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.






 SIGUIENTE
SIGUIENTE